9.5 Методи та моделі багатовимірного шкалювання

Мета

Закріплення теоретичного та практичного матеріалу за темою «Моделі багатовимірного шкалювання»; набуття навичок роботи в модулі Multidimensional Scaling.

Завдання

Необхідно провести шкалювання простору ознак для вибіркових даних у модулі Multidimensional Scaling ППП Statistica:

1. Побудувати матричний файл зі структурою відповідно до постановки задачі.
2. Оцінити параметри якості моделей для різних типів шкального простору.
3. Побудувати шкальний простір ознак, вибрати остаточний варіант розбивки на шкали, зробити висновки щодо характеру шкалювання.
4. Представити результати графічного аналізу дослідження якості моделі (графік простору, діаграма Шепарда, графіки монотонних перетворень).
5. Зробити висновки щодо угрупування об’єктів за шкальним простором, дати інтерпретацію отриманих результатів і компонентного складу латентних шкал.

Література: [5–9; 14; 41–44; 48; 49; 76].

Методичні рекомендації

Для розв’язання задач дослідження просторової структури даних об’єктів у ППП Statistica існує особливий набір підпрограм, об’єднаних у групу методів Multidimensional Scaling (Багатовимірне шкалювання). У модулі можна отримати розрахунки за метричними та неметричними методами багатовимірного шкалювання, заснованими на інформації про подібності або відмінності досліджуваних об’єктів. Розглянемо порядок роботи в даному модулі.

Щоб запустити модуль Multidimensional Scaling, необхідно в даному середовищі створити матричний файл, що має таку структуру:

• кількість спостережень повинна дорівнювати числу змінних плюс чотири допоміжні рядки;
• матриця повинна бути квадратною, імена спостережень мають збігатися з іменами змінних;
• останні чотири спостереження повинні містити таку інформацію:
  • Means — для кожної змінної обчислюється середнє значення. Дана операція здійснюється за допомогою команди Statistics of Block Data / Block columns / Means;
  • Std. Dev. — для кожної змінної обчислюється середнє квадратичне відхилення за допомогою команди Statistics of Block Data / Block columns / St’s;
  • No. Cases — кількість показників, на основі яких була розрахована відповідна матриця;
  • Matrix — даний рядок може приймати чотири значення: 1 — матриця кореляцій; 2 — матриця відстаней; 3 — матриця відмінностей; 4 — матриця коваріацій.

Отриманий матричний файл перетворюється на великоформатну таблицю за допомогою команди Format / Spreadsheets / System Default, доступну за запуском стартової панелі програми. Приклад перетворених вихідних даних для роботи в модулі поданий на рис. 9.77.

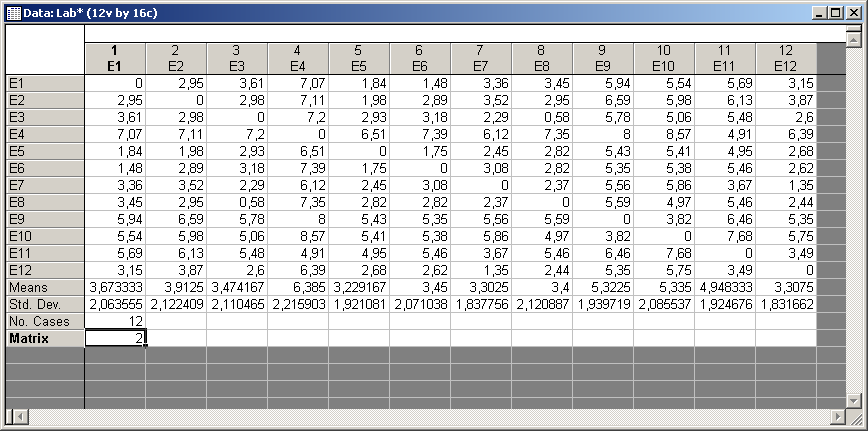
Рис. 9.77: Вихідні дані

Щоб приступити до обчислювальних процедур, необхідно ввійти в позицію меню Statistics / Multivariate Exploratory Techniques / Multidimensional Scaling (рис. 9.78).

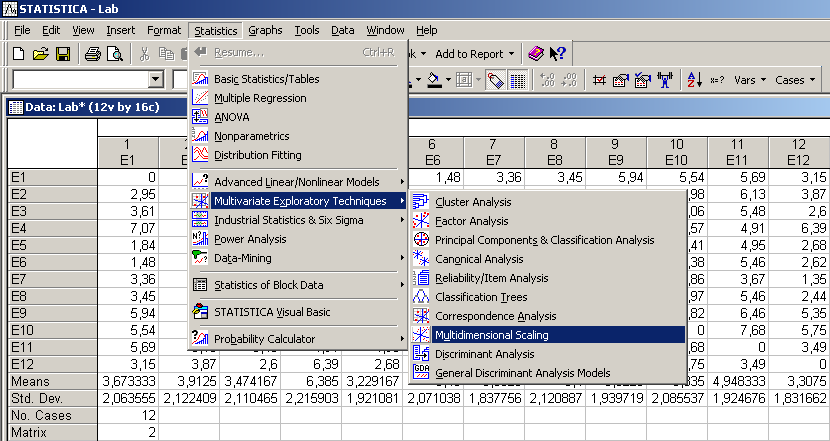
Рис. 9.78: Вибір модуля

Після запуску модуля з’явиться його стартова панель, де необхідно задати змінні для аналізу (Variables) і вибрати початковий розмір шкального простору (Number of dimensions) (рис. 9.79).

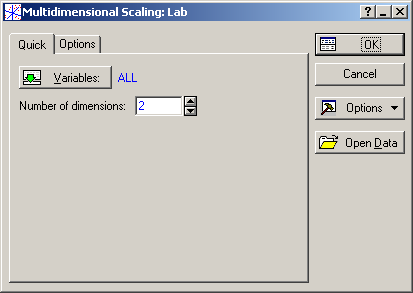
Рис. 9.79: Стартова панель модуля

У закладці (Options) задається стартова конфігурація для розрахунків. У розглянутому прикладі задана стандартна конфігурація моделі за Гутманом (рис. 9.80).

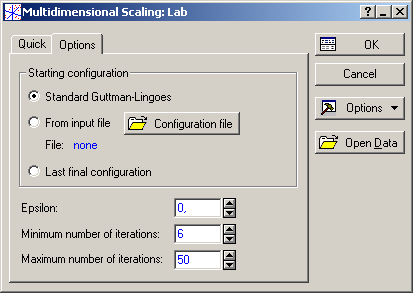
Рис. 9.80: Стартова конфігурація

Натисніть кнопку ОК, і перед вами з’явиться вікно, що містить параметри оцінювання (рис. 9.81). Оскільки визначення параметрів — ітеративна процедура, то у вікні будуть виділені найкращі значення параметрів конфігурації заданого розміру, а також подана інформація про збіжність процедури оцінювання (Estimation procedure converged).

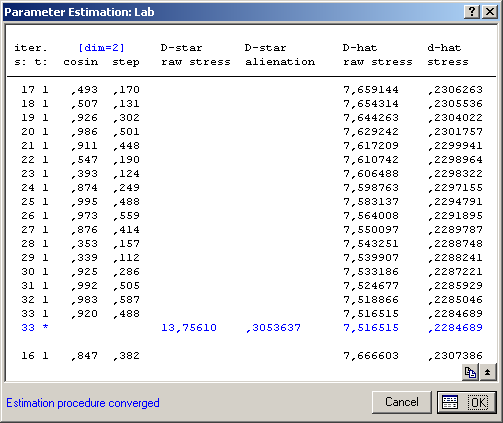
Рис. 9.81: Вікно параметрів оцінювання

Натисніть кнопку ОК для перегляду результатів аналізу. У верхній частині отриманого вікна міститься основна інформація про якість моделі: Vars from file (кількість змінних), Number of dimensions (кількість шкал), Start config. (стартова конфігурація моделі), Last iteration (остання ітерація), Best iteration (найкраща ітерація). Далі подані всі коефіцієнти для найкращої ітерації D-star: Raw stress (значення стресу за Гутманом), D-hat: Raw stress (значення стресу за Краскалом), Alienation (коефіцієнт відчуження), Stress (значення стресу). У нижній частині вікна знаходиться ряд опцій, кожна з яких пов’язана з певним напрямом аналізу побудованої моделі (рис. 9.82).

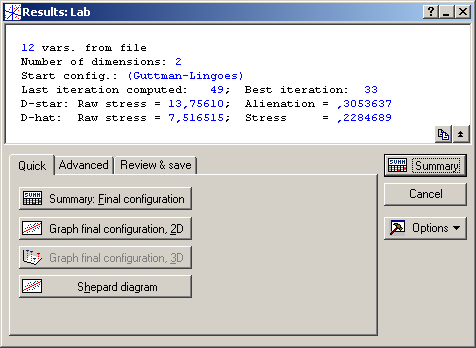
Рис. 9.82: Вікно оцінки параметрів для двовимірного простору

Подальше дослідження моделі спрямоване на виявлення оптимального числа латентних ознак (шкал), на які необхідно розбити вихідну сукупність. Кількість шкал визначається за мінімальним значенням стресу для відповідного шкального простору, однак чим більше шкал, тим менше значення стресу. Значення показників стресу для досліджуваної моделі розміщені на рис. 9.83.

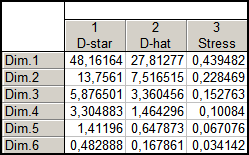
Рис. 9.83: Залежність значень стресу від розміру простору

Для визначення оптимальної розмірності використовують графік залежності стресу від різної кількості шкал (графік «кам’янистого осипу») (рис. 9.84).

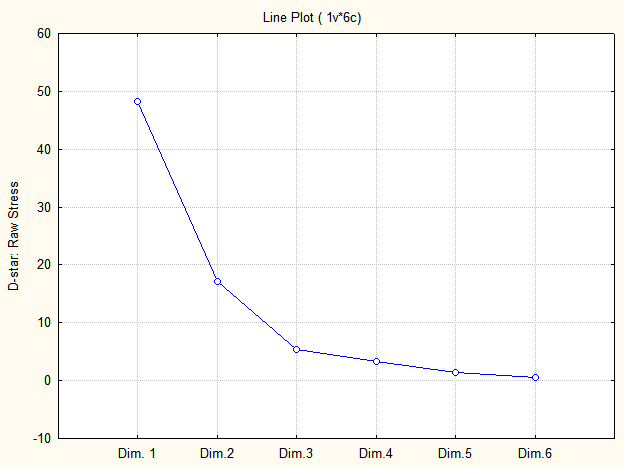
Рис. 9.84: Графік «кам’янистого осипу»

Висновок про розмірність можна зробити, знайшовши таку абсцису на графіку, в якій графік стресу починає візуально згладжуватися в напрямку правої, пологої його частини; таким чином, зменшення стресу максимально сповільнюється. Відповідно до даного критерію варто вибрати для відтворення моделі тривимірний простір.

Проведемо аналіз моделі тривимірного простору. Для цього у вікні початкових умов виберемо трирівневу розмірність. Після цього буде створена початкова конфігурація і відкрите вікно оцінки параметрів. Натиснувши кнопку Summary: Final configuration, отримуємо матрицю координат стимулів (рис. 9.85).

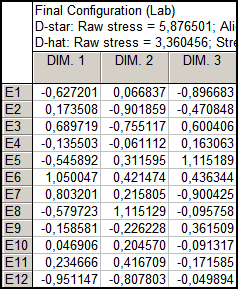
Рис. 9.85: Матриця координат стимулів

Саме ці координати відображають просторовий розподіл підприємств у тривимірному просторі, графік якого можна створити, натиснувши клавішу Graf Final configuration, 3D (рис. 9.86).

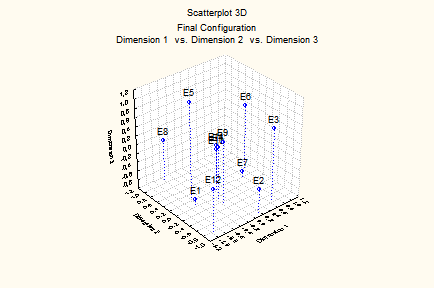
Рис. 9.86: Просторовий розподіл підприємств

Для оцінювання залежності відтворених відстаней від вихідних використовують діаграму Шепарда (рис. 9.87). На осі ординат діаграми позначені відтворені відстані, а на осі абсцис відкладаються істинні подібності між об’єктами. На цьому графіку також відображається графік степеневої функції, що містить величини D-hats, тобто результат монотонного перетворення вихідних даних за Краскалом.

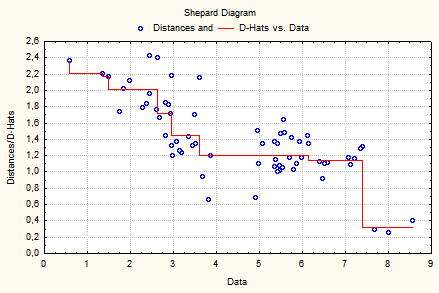
Рис. 9.87: Діаграма Шепарда

Якби всі відтворені результативні відстані лягли на степеневу лінію, то ранги спостережуваних відстаней були б у точності відтворені отриманим рішенням (просторовою моделлю). Відхилення від цієї лінії показують на погіршення якості згоди (тобто якості підгонки моделі). Щоб оцінити якість тривимірного рішення, необхідно проаналізувати таблицю фактичних і оцінюваних відстаней. Для цього, натиснувши кнопку Summary statistics, створимо таблицю (рис. 9.88), що містить чотири стовпці. У першому стовпці зазначено, між якими об’єктами обчислена дана відстань. У другому стовпці відображені відтворені для даної конфігурації відстані. Стовпці D-hat і D-star — монотонні перетворення вихідних даних: D-star відображає перетворення за Гутманом, а D-hat — регресію, оцінювану за Краскалом.

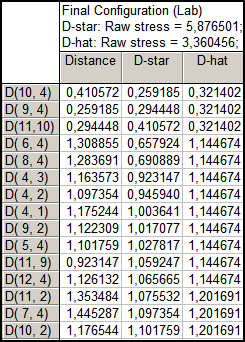
Рис. 9.88: Таблиця відтворених і перетворених відстаней

Рядки таблиці містять відстані, визначені в матриці відмінностей, відсортовані за величиною D-star або D-hat. Якщо якість даної моделі (кількість шкал) досить добра, то порядок відтворених відстаней приблизно дорівнює перетвореним вихідним даним (тобто або величині D-star, або D-hat). Наявність дуже відмінних елементів з упорядкування свідчить про недостатню точність моделі. Аналіз наведеної таблиці свідчить про задовільну якість моделі, тому що немає значних відмінностей у значеннях відтворених і перетворених даних.

Додатково якість підгонки моделі можна проілюструвати графіками перетворення даних D-hats і D-stars, (графіки створюємо, натисканням кнопок D-hat values і D-star values) (рис. 9.89, 9.90).

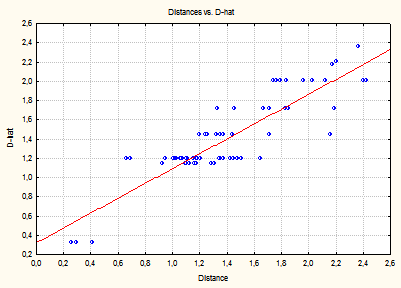
Рис. 9.89: Графік монотонного перетворення за Краскалом

Із графіків видно, що майже всі точки згруповані навколо ліній монотонних перетворень. Це може свідчити про те, що тривимірна конфігурація досить адекватно описує подібності між об’єктами.

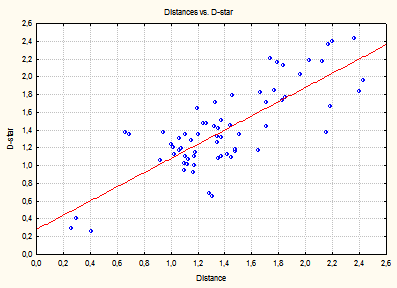
Рис. 9.90: Графік монотонного перетворення за Гутманом

Проведений аналіз тривимірної моделі шкального простору дає адекватну оцінку якості моделі, тобто розміщення підприємств із даними характеристиками в тривимірному просторі найбільш обґрунтоване та має логічну економічну інтерпретацію. Для визначення компонентного складу векторів необхідно застосувати факторний аналіз і визначити, які вихідні показники сформували латентні фактори, або шкали.