9.4 Методи редукції

Мета: Закріплення теоретичного та практичного матеріалу за темою «Методи редукції»; набуття навичок вибору показників-репрезентантів і побудови таксономічного показника рівня розвитку в середовищі Microsoft Excel.

Завдання 1

Необхідно вибрати найбільш значущі для оцінювання стабільності фінансового стану досліджуваних підприємств показники (показники-репрезентанти) за допомогою методу «центра ваги»:

Стандартизувати вихідні дані.
Розрахувати матриці евклідових відстаней для кожної групи фінансових показників.
Вибрати на основі суми відстаней показник-репрезентант у кожній групі фінансових показників, дати економічну інтерпретацію отриманим результатам.

Завдання 2

Необхідно здійснити впорядкування підприємств за стабільністю фінансового стану на основі методу рівня розвитку:

На основі стандартизованих вихідних даних визначити еталон розвитку для досліджуваних підприємств.
Розрахувати евклідові відстані між окремими підприємствами та еталоном.
Розрахувати таксономічний показник рівня розвитку на основі евклідових відстаней для кожного досліджуваного підприємства.
Здійснити впорядкування підприємств за стабільністю фінансового стану на основі таксономічного показника рівня розвитку, дати економічну інтерпретацію отриманим результатам.

Література: [5–9; 14; 41–44; 48; 49; 76].

Методичні рекомендації

Завдання 1

У багатьох економічних дослідженнях виникає потреба в зменшенні числа ознак, що описують досліджувану область дійсності. Однак зі скороченням числа змінних повинні дотримуватися деякі вимоги для того, щоб створений опис не спотворював дійсності. Існує досить великий спектр методів багатовимірного аналізу, що дозволяє розв’язувати завдання зі скорочення розмірності простору ознак. Такі методи підрозділяють на дві групи: методи побудови узагальнених показників, методи зменшення числа ознак.

Перша група методів спрямована на обчислення інтегральної оцінки об’єктів, що мають багатоознакову природу, у вигляді деякої функції \(f(y_1,y_2,…y_q)\), що відбиває вплив усіх ознак. Такий спосіб дозволяє впорядкувати досліджувані об’єкти.

Сутність роботи другої групи методів полягає в заміні первісного набору \(q\) ознак \(y=(y_1,y_2,…y_q)\) набором \(s\) діагностичних ознак \(x=(x_1,x_2,…x_m)(s<q)\), які мають такі властивості: ознаки не корельовані або слабо корельовані між собою; сильно корельовані з ознаками, що не входять у діагностичний набір. Таким чином, друга група методів дозволяє виключити з первісної системи ознак ті, які дублюють інформацію, а також забезпечує вибір ознак, що найбільш повно відображають стан досліджуваних процесів.

Одним з методів другої групи є метод «центра ваги». Розглянемо порядок розрахункових процедур для вибору показників-репрезентантів на основі алгоритму даного методу в середовищі Microsoft Excel.

Алгоритм методу «центра ваги» містить такі основні кроки.

Крок 1. На першому кроці алгоритму формуються матриці вхідних даних за кожною групою показників стану об’єкта дослідження \(y_1,y_2,…y_q\), де \(q\) — кількість груп показників. Для \(k\)-ї групи показників структура цієї матриці може бути визначена таким чином: \(y_k=(y_{ij}),i=[1;m], [1;n]\), де \(y_{ij}\) — значення \(i\)-го показника в \(j\)-му досліджуваному періоді; \(m\) — кількість показників, що входять у \(k\)-ту групу; \(n\) — кількість досліджуваних періодів.

Вхідні дані для вибору показників-репрезентантів наведені на рис. 9.60: \(x_1\) — коефіцієнт поточної ліквідності, \(x_2\) — коефіцієнт швидкої ліквідності, \(x_3\) — коефіцієнт абсолютної ліквідності, \(x_4\) — коефіцієнт забезпеченості власними оборотними коштами, \(x_5\) — коефіцієнт маневреності власного капіталу, \(x_6\) — коефіцієнт заборгованості, \(x_7\) — коефіцієнт оборотності активів, \(x_8\) — коефіцієнт оборотності оборотних коштів, \(x_9\) — коефіцієнт оборотності запасів, \(x_{10}\) — коефіцієнт рентабельності активів, \(x_{11}\) — коефіцієнт рентабельності власного капіталу.

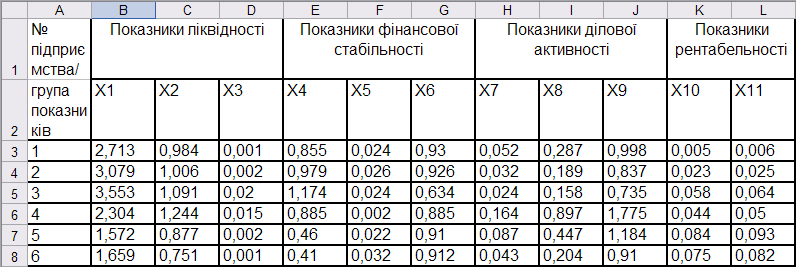
Рис. 9.60: Вихідні дані

Крок 2. Оскільки показники можна виразити в абсолютних і відносних величинах, а також мати різні одиниці вимірювання, то на другому кроці здійснюється процедура їхньої стандартизації за формулою:

\[ z_{ij} = \frac{y_{ij} - \bar{y}_i}{s_i}, \]

де \(z_{ij}\) — стандартизоване значення \(i\)-го показника в \(j\)-му досліджуваному періоді;

\(\bar{y}_i\) — середнє арифметичне значення \(i\)-го показника;

\(s_i\) — стандартне відхилення \(i\)-го показника.

Для стандартизації вихідних даних спочатку необхідно розрахувати середнє арифметичне значення \(i\)-го показника та стандартне відхилення \(i\)-го показника в середовищі Microsoft Excel за допомогою функцій СРЗНАЧ і СТАНДОТКЛОН, як це показано на рис. 9.61.

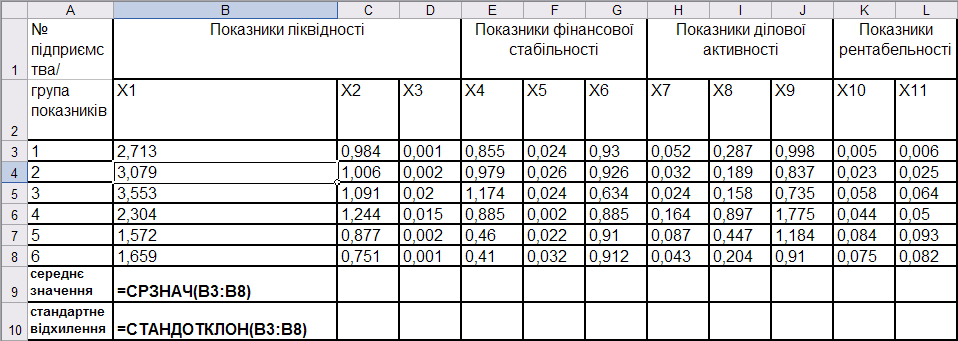
Рис. 9.61: Розрахунок середнього арифметичного та стандартного відхилення значення \(i\)-го показника

Результати розрахунку показників наведені на рис. 9.62.

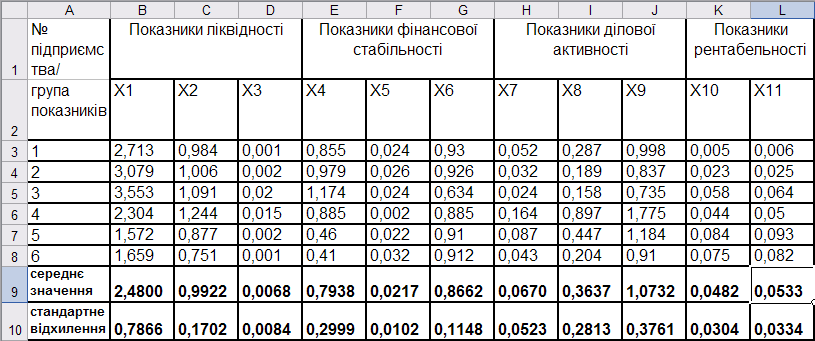
Рис. 9.62: Результати розрахунку середнього арифметичного та стандартного відхилення значення \(i\)-го показника

Для стандартизації вихідних даних необхідно створити таблицю такої ж розмірності, як таблиця вхідних даних. Стандартизацію вихідних даних в середовищі Microsoft Excel можна здійснити за допомогою функції НОРМАЛИЗАЦИЯ, аргументами якої є вихідні дані, середнє значення та стандартне відхилення показників (рис. 9.63).

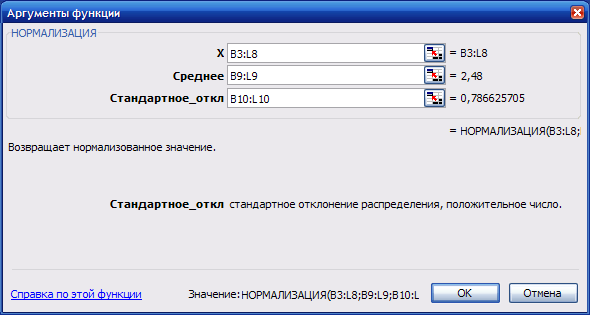
Рис. 9.63: Аргументи функції НОРМАЛИЗАЦИЯ

Для стандартизації вихідних даних необхідно в першій комірці створеної таблиці задати аргументи функції НОРМАЛИЗАЦИЯ; потім, починаючи з першої комірки, виділити діапазон, в якому будуть розраховані стандартизовані дані; натиснути клавішу F2, а потім одночасно натиснути клавіші Ctrl + Shift + Enter (рис. 9.64).

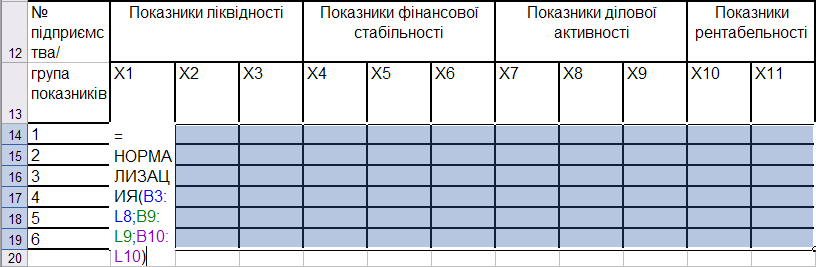
Рис. 9.64: Розрахунок стандартизованих значень показників

Результати стандартизації наведені на рис. 9.65.

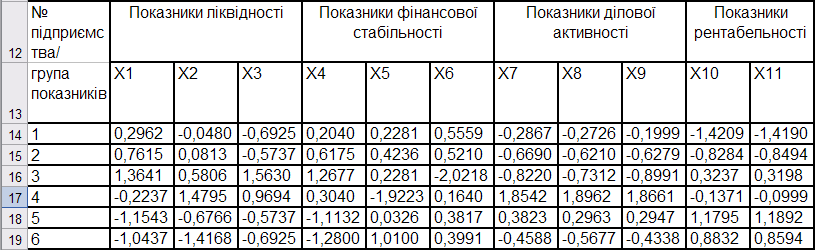
Рис. 9.65: Таблиця стандартизованих значень показників

Крок 3. Описані обчислювальні процедури є основою для розрахунку матриць відстаней \(p_1,p_2,…p_q\), елементи яких відбивають ступінь близькості показників усередині кожної групи. Як міра відстані використовується евклідова відстань, що визначається за формулою:

\[ \rho_E(z_i,z_j) = \sqrt{\sum_{l=1}^n(z_{ij}-z_{jl})^2}, \]

де \(\rho_E (z_i,z_j)\) — відстань між \(i\)-м і \(j\)-м показником групи;

\(z_{il}\), \(z_{jl}\) — стандартизовані значення \(i\)-го та \(j\)-го показників групи в періоді \(l\).

Матриці відстаней розраховуються для груп з числом показників більше двох. Це групи показників ліквідності, фінансової стабільності та ділової активності. Розрахунок відстаней для показників ліквідності наведено на рис. 9.66.

Матриця відстаней показників є симетричною з нульовими діагональними елементами (оскільки відстань від показника до самого себе дорівнює нулю).

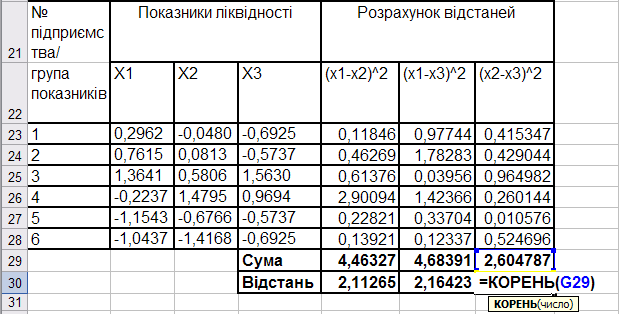
Рис. 9.66: Розрахунок відстаней для показників ліквідності

Матриця відстаней для групи показників ліквідності наведена на рис. 9.67.

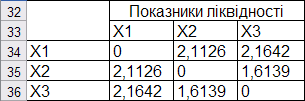
Рис. 9.67: Матриця відстаней для групи показників ліквідності

Аналогічно розраховуються матриці відстаней для груп показників фінансової стабільності та ділової активності (рис. 9.68).

Рис. 9.68: Матриці відстаней для груп показників фінансової стабільності та ділової активності

Крок 4. На четвертому кроці здійснюється вибір так званих показників-репрезентантів груп, які містять найбільш значущу інформацію, властиву групі за правилами:

у групах з одного елемента показники, що їх утворюють, мають властивості, які сильно відрізняються від показників інших груп; тому вони належать до числа показників-еталонів (репрезентантів);
у групах, де число показників більше двох, розраховується сума відстаней кожного показника до інших показників групи: \[ \rho_i=\sum_{j=1, j\neq i}^m \rho (z_i, z_j), \]

де \(m\) — кількість показників групи.

До складу показників-репрезентантів належить показник з найменшою сумою відстаней: \(ρ_s = \min_i \rho_i\).

У групах, які складаються з двох показників, спочатку обчислюють суму відстаней показників, що належать до групи, від показників-репрезентантів, вибраних за описаними правилами: \(\rho_i=\sum_{j=1, j\neq i}^k \rho (z_i, z_j)\), де \(k\) — кількість груп показників. Репрезентантом є той показник, у якого сума відстаней до виокремлених репрезентантів інших груп елементів є максимальною: \(ρ_s = \max_i \rho_i\).

Таким чином, результатом четвертого кроку є набір показників-репрезентантів \(x=(x_1,x_2,…x_k)\), що описують найбільш важливі аспекти стану об’єкта дослідження.

У таблиці вхідних даних відсутні групи з одним елементом, отже пропустимо цей крок і розглянемо групи з числом показників більше двох. Розрахуємо суми відстаней та виберемо показники-репрезентанти у цих групах на основі найменшої суми відстаней (рис. 9.69).

Отже, як показник-репрезентант у групі показників ліквідності був виділений показник швидкої ліквідності \((x_2)\); у групі показників фінансової стабільності — коефіцієнт маневреності власного капіталу \((x_5)\); у групі показників ділової активності — коефіцієнт оборотності активів \((x_7)\).

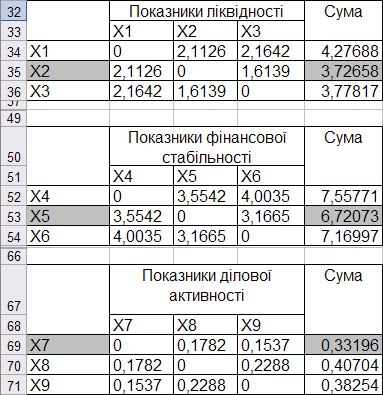
Рис. 9.69: Вибір показників-репрезентантів груп з кількістю показників більше двох

Оскільки група показників рентабельності включає тільки два показники, то для вибору показника-репрезентанта цієї групи знайдемо відстані від кожного показника до раніше виділених показників-репрезентантів (рис. 9.70). Як показник-репрезентант вибирається той, у якого сума відстаней від показників-репрезентантів, виділених із груп елементів із числом більше двох, максимальна.

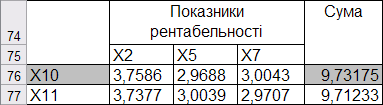
Рис. 9.70: Вибір показника-репрезентанта групи, де кількість показників дорівнює двом

Максимальною є сума відстаней від коефіцієнта рентабельності активів \((x_{10})\) до вибраних раніше репрезентантів. Отже, цей показник і буде репрезентантом групи показників рентабельності.

Таким чином, до показників-репрезентантів відносять: показник швидкої ліквідності \((x_2)\), коефіцієнт маневреності власного капіталу \((x_5)\), коефіцієнт оборотності активів \((x_7)\), коефіцієнт рентабельності активів \((x_{10})\).

Завдання 2

Для зіставлення об’єктів, які характеризуються більшою кількістю ознак, найчастіше застосовують таксономічні процедури. Одним з методів дослідження багатовимірних об’єктів є таксономічний показник рівня розвитку, запропонований З. Хельвігом. Це синтетична величина, «рівнодіюча» всіх ознак, що характеризують об’єкти, яка дозволяє лінійно впорядкувати елементи досліджуваної сукупності.

Першим кроком процесу побудови таксономічного показника рівня розвитку є визначення елементів матриці спостережень:

\[ X = \left(\begin{array}{c}x_{11} & x_{12} & … & x_{1j} & …& x_{1m} \\ x_{21} & x_{22} & … & x_{2j} & … & x_{2m} \\ … & … & … & … & … & … \\ x_{i1} & x_{i2} & … & x_{ij} & … & x_{im} \\ … & … & … & … & … & … \\ x_{ω1} & x_{ω1} & … & x_{ωj} & … & x_{ωm}\end{array}\right), \]

де \(ω\) — кількість досліджуваних об’єктів;

\(m\) — кількість ознак;

\(x_{ij}\) — значення \(j\)-ї ознаки для \(i\)-го об’єкта.

Оскільки ознаки, що включаються в матрицю спостережень, неоднорідні, то проводять стандартизацію їх значень. Матриця стандартизованих вихідних даних наведена на рис. 9.65.

Наступний крок у розглянутій процедурі полягає в диференціації ознак матриці спостережень. Усі змінні розподіляють на стимулятори та дестимулятори. Підставою розподілу ознак на дві групи є характер впливу кожного з них на рівень розвитку досліджуваних об’єктів. Ознаки, що чинять позитивний, стимуляційний вплив на рівень розвитку об’єктів, називають стимуляторами, на відміну від ознак-дестимуляторів (табл. 9.1).

Табл. 9.1: Класифікація ознак на стимулятори та дестимулятори
Умовне позначення показника	Показники	Характер впливу на рівень стабільності фінансового стану	Група
\(x_1\)	Коефіцієнт поточної ліквідності	Позитивний	Стимулятор
\(x_2\)	Коефіцієнт швидкої ліквідності	Позитивний	Стимулятор
\(x_3\)	Коефіцієнт абсолютної ліквідності	Позитивний	Стимулятор
\(x_4\)	Коефіцієнт забезпеченості власними оборотними коштами	Позитивний	Стимулятор
\(x_5\)	Коефіцієнт маневреності власного капіталу	Позитивний	Стимулятор
\(x_6\)	Коефіцієнт заборгованості	Негативний	Дестимулятор
\(x_7\)	Коефіцієнт оборотності активів	Позитивний	Стимулятор
\(x_8\)	Коефіцієнт оборотності оборотних коштів	Позитивний	Стимулятор
\(x_9\)	Коефіцієнт оборотності запасів	Позитивний	Стимулятор
\(x_{10}\)	Коефіцієнт рентабельності активів	Позитивний	Стимулятор
\(x_{11}\)	Коефіцієнт рентабельності власного капіталу	Позитивний	Стимулятор

Розподіл ознак на стимулятори та дестимулятори є основою для побудови так званого еталона розвитку, що є точкою з координатами:

\[ P_0(z_{01} z_{02},…,z_{0s},…,z_{0m}), \]

де \(z_{0s}=\max_r z_{rs}\), якщо \(s∈I\);

\(z_{0s}=\min_r z_{rs}\), якщо \(s∉I, (s = 1,...,m)\);

де \(I\) — множина стимуляторів;

\(z_{rs}\) — стандартизоване значення ознаки \(s\) для об’єкта \(r\).

Визначення еталона розвитку в середовищі Microsoft Excel здійснюється за допомогою функцій МАКС і МИН (рис. 9.71).

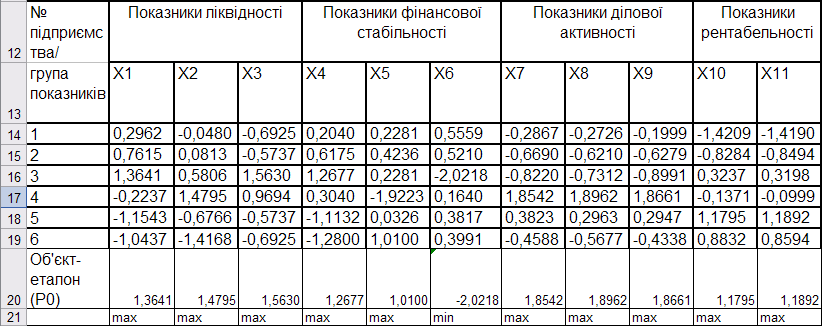
Рис. 9.71: Визначення еталона розвитку

Відстань між окремими точками-одиницями та точкою \(P_0\), що є еталоном розвитку, позначається \(c_{i0}\) і розраховується на основі евклідової відстані за формулою:

\[ \rho_{i0} = \sqrt{\sum_{j=1}^{m}(z_{ij} - z_{0j})^2}. \]

Розрахунок відстаней між окремими підприємствами й об’єктом-еталоном наведено на рис. 9.72.

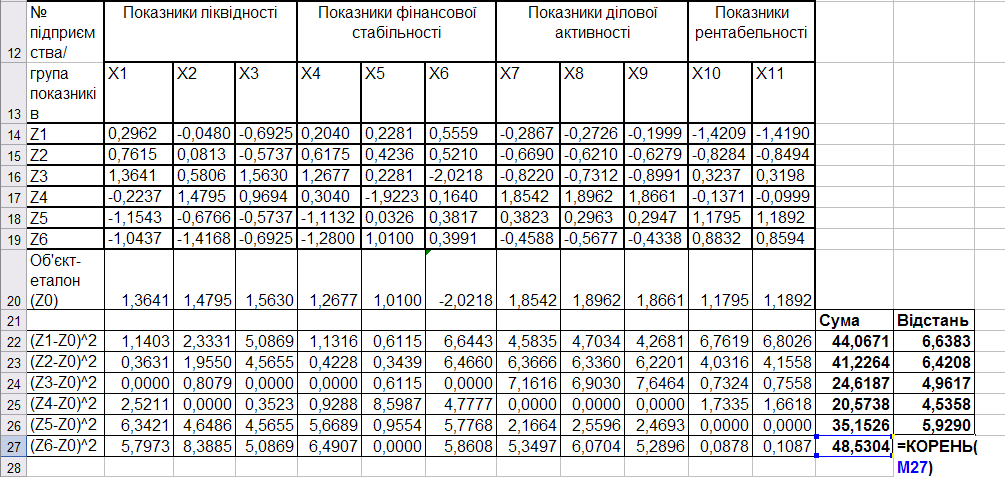
Рис. 9.72: Розрахунок відстаней між окремими підприємствами й об’єктом-еталоном

Результати розрахунку евклідових відстаней від кожного підприємства до еталону наведені на рис. 9.73.

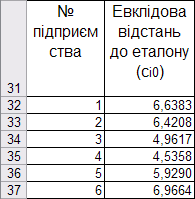
Рис. 9.73: Евклідові відстані від кожного підприємства до еталона

Отримані відстані слугують вихідними величинами, що використовуються для розрахунку показника рівня розвитку:

\[ d_i^* = 1 - \frac{c_{i0}}{c_0}, \\ c_0 = \bar{c}_0 + 2s_0; \bar{c}_0 = \frac{1} \sum_{i=1}^w c_{i0}; s_0 = \sqrt{\frac{1}{w} \sum_{i=1}^w(c_{i0}-\bar{c}_0 )^2}. \]

Розрахунок показника рівня розвитку наведено на рис. 9.74.

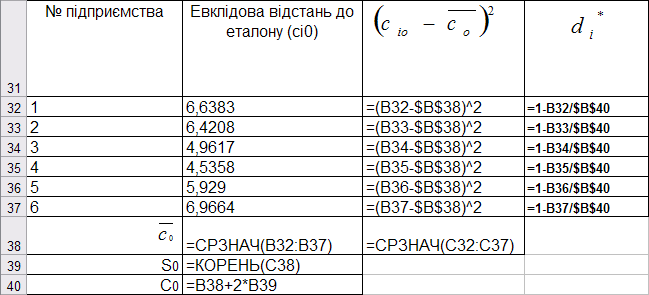
Рис. 9.74: Розрахунок таксономічного показника рівня розвитку

Отримані результати розрахунку наведені на рис. 9.75.

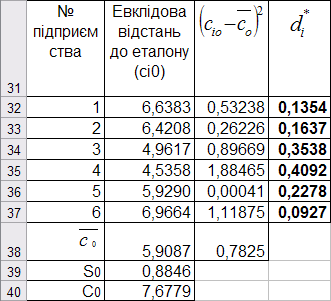
Рис. 9.75: Значення таксономічного показника рівня розвитку підприємств

Інтерпретація показника рівня розвитку є такою: чим ближче значення показника рівня розвитку до одиниці, тим на більш високому рівні розвитку перебуває об’єкт.

Упорядкуємо підприємства за рівнем розвитку (рис. 9.76).

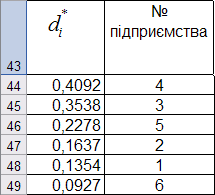
Рис. 9.76: Упорядковані підприємства за рівнем розвитку

Таким чином, найбільш стійким є четверте підприємство, а найгірше фінансове становище характерне для шостого.