9.3 Методи та моделі дискримінантного аналізу. Класифікація з навчанням

Мета

Закріплення теоретичного та практичного матеріалу за темою «Методи та моделі дискримінантного аналізу»; набуття навичок роботи в модулі Discriminant Analysis.

Завдання

Необхідно побудувати модель класифікації підприємств і провести розпізнавання для вибіркових даних у модулі Discriminant Analysis ППП Statistica:

1. Побудувати модель дискримінантного аналізу на основі вибіркових даних.
2. Дати оцінку якості моделей розпізнавання, значущості змінних та провести канонічний аналіз функцій.
3. Побудувати моделі, використовуючи методи покрокового аналізу включення та виключення факторних змінних; дати оцінку якості побудованих моделей та дискримінації змінних.
4. Проаналізувати результати розпізнавання (матриця класифікацій), подати теоретичну класифікацію за дискримінантною моделлю.
5. Зробити висновки та прогнози (розпізнавання) за побудованою моделлю. Дати економічну інтерпретацію отриманим результатам.

Література: [5–9; 14; 41–44; 48; 49; 76].

Методичні рекомендації

Для розв’язання та аналізу задач класифікації багатомірних сукупностей за наявності навчальних вибірок (класифікація з навчанням) у ППП Statistica передбачений модуль Discriminant Analysis (Дискримінантний аналіз). Розглядуваний модуль має широкий набір засобів, які забезпечують проведення дискримінантного аналізу даних, візуалізації та інтерпретації результатів. Розглянемо порядок роботи в даному модулі. Таблиця вихідних даних для розв’язання задачі розміщена на рис. 9.35.

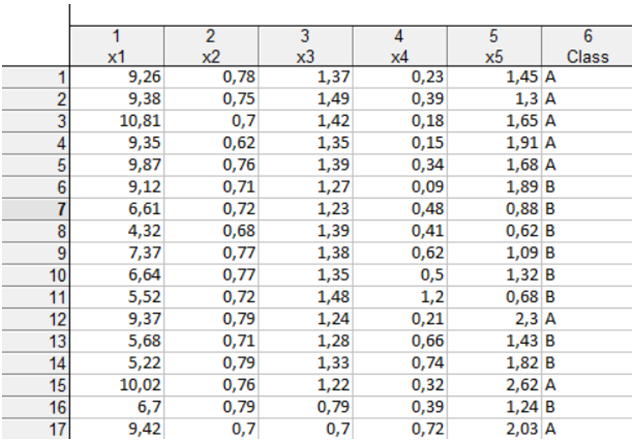
Рис. 9.35: Вхідні дані

В якості факторів впливу на рівень інвестиційної привабливості розглядаються такі коефіцієнти: \(x_1\) — продуктивність праці; \(x_2\) — питома вага робітників у складі промислово-виробничого персоналу; \(x_3\) — коефіцієнт змінності; \(x_4\) — коефіцієнт браку ; \(x_5\) — коефіцієнт фондовіддачі ОВФ. Значення показників розподілене на навчальні вибірки (група А — інвестиційно привабливі підприємства, група В — підприємства-аутсайдери). Щоб перейти до обчислювальних процедур, необхідно ввійти в меню Statistics / Multivariate Exploratory Techniques / Disсriminant Analysis (рис. 9.36).

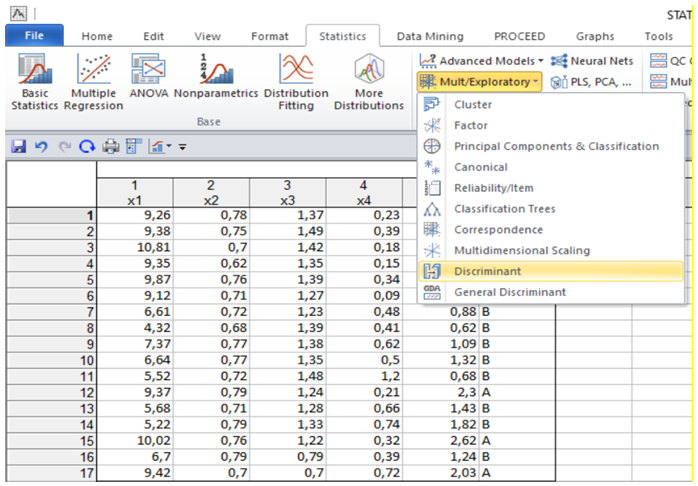
Рис. 9.36: Вибір модуля

Після підтвердження вибору модуля перед вами з’явиться стартова панель модуля, де необхідно задати вихідні параметри моделювання (рис. 9.37).

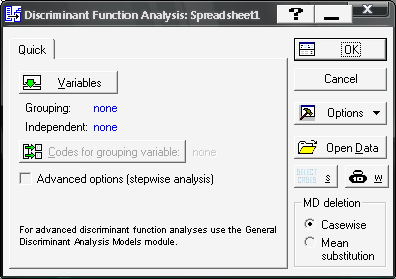
Рис. 9.37: Стартова панель модуля

Натисніть кнопку Variables (Змінні); у вікні, що з’явилося, вкажіть показники, за якими будете здійснювати аналіз (рис. 9.38). Після вибору залежних (групувальна — залежна змінна) та незалежних змінних підтвердіть свій вибір натисканням кнопки OK. Також у вікні можна задати коди для значень групувальної змінної.

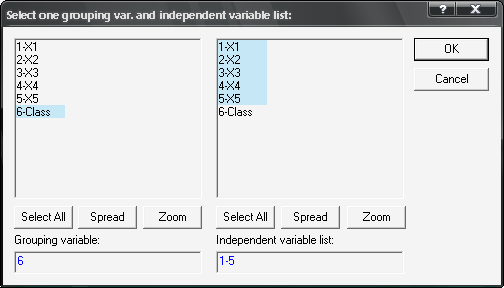
Рис. 9.38: Вибір змінних для аналізу

Стартова панель модуля Disсriminant Analysis з опціями для аналізу наведена на рис. 9.39.

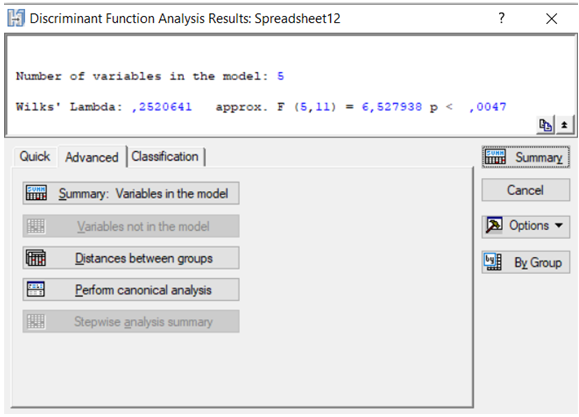
Рис. 9.39: Результати дискримінантного аналізу

У верхній інформаційній частині вікна показані значення лямбди Уїлкса (\(\lambda\)), яка характеризує якість дискримінації та змінюється в межах \([0,1]\). Близькі до нуля значення визначають гарну якість дискримінації. Значення критерію Фішера (\(F\)) — оцінки адекватності моделі наведено для порівняння з табличними значеннями.

У нижній частині вікна подано різноманітні опції для досконалого аналізу моделі та побудови графіків. Обравши опцію Summary: Variables in the model (Аналіз змінних у моделі) на вкладці Advanced, отримаємо результати дискримінантного аналізу, наведені на рис. 9.40.

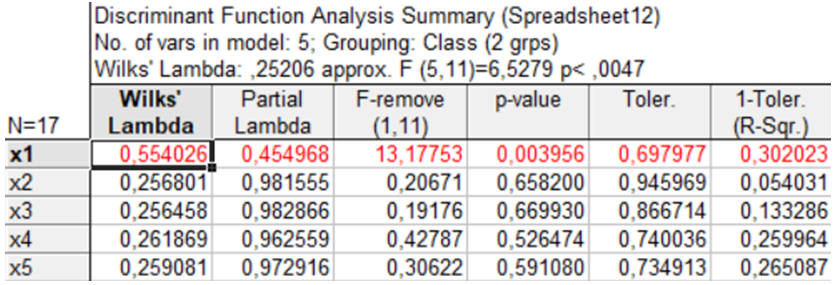
Рис. 9.40: Результати дискримінантного аналізу

Розглянемо стовпці таблиці:

• Wilks’ Lambda (лямбда Уїлкса) — лямбда Уїлкса, яка є результатом виключення відповідної змінної з моделі. Чим більше значення лямбди Уїлкса, тим більш значуща змінна в процедурі дискримінації;
• Partial Lambda (частинна лямбда) — характеризує одиничний внесок відповідної змінної в дискримінацію моделі. Чим менше дана статистика, тим більший її вклад у загальну дискримінацію;
• F-remove (F-виключення) — значення \(F\)-критерію для відповідної змінної;
• p-value (рівень значущості) — рівень статистичної значущості змінної;
• Toler (толерантність) — визначається як \((1 - R^2)\), де \(R^2\) — коефіцієнт множинної кореляції даної змінної зі всіма іншими змінними в моделі. Толерантність є мірою збитковості змінних у моделі.

Таким чином, можна дійти висновку, що найбільш значущою змінною для дискримінації є змінна \(x_1\). Натиснувши клавішу Distances between groups (Відстані між групами), отримаємо таблицю відстаней (рис. 9.41), яка характеризує якість дискримінації спостережень і ступінь відмінностей (неоднорідність) груп.

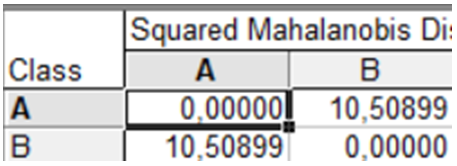
Рис. 9.41: Матриця відстаней між групами

З натисканням на опцію Perform canonical analysis (Канонічний аналіз) відкриється меню напрямів канонічного аналізу (рис. 9.42).

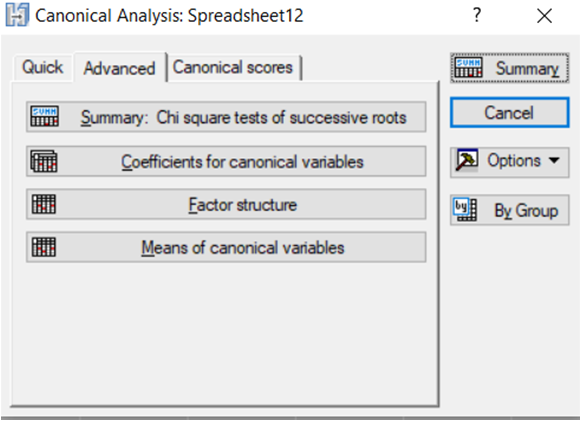
Рис. 9.42: Опції канонічного аналізу функцій

Summary: Chi square tests of successive roots (Підсумки: \(\chi\)-критерій послідовності коренів) (рис. 9.43).

Рис. 9.43: Критерій канонічних коренів

Отримані результати дозволяють провести оцінювання кількості значущих коренів для інтерпретації та статистичну значущість дискримінантних функцій.

Coefficients for canonical variables (Коефіцієнти канонічних змінних). Ініціювання даної опції дозволяє отримати таблиці нестандартизованих і стандартизованих коефіцієнтів дискримінантних функцій (рис. 9.44).

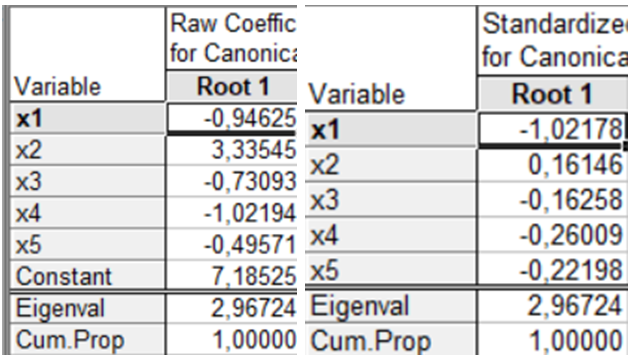
Рис. 9.44: Коефіцієнти канонічних змінних

Ці результати використовують для визначення значень канонічних змінних для кожного спостереження, а також ступеня та напряму впливу змінних у кожній дискримінантній функції. Factor structure — факторна структура. У таблиці на рис. 9.45 показані об’єднані внутрішньогрупові кореляції змінних з відповідними дискримінантними функціями, які використовуються для змістовної інтерпретації функцій. Means of canonical variables (Середні значення канонічних змінних) (рис. 9.45) містить середні значення для дискримінантних функцій, які дозволяють визначити групи, які найкраще ідентифікуються конкретною дискримінантною функцією.

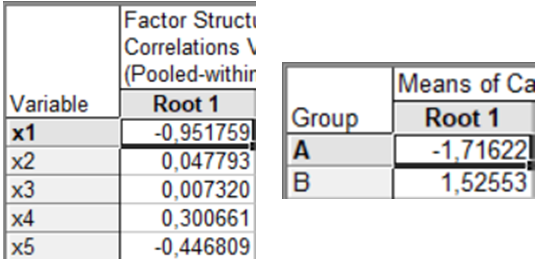
Рис. 9.45: Факторна структура та середні значення канонічних змінних

Для побудови дискримінантних функцій необхідно ініціювати опцію Classification functions (Функції класифікації) на вкладці (Classification) (рис 9.46).

Рис. 9.46: Опції результатів класифікації

Дискримінантні функції для виділених класів станів підприємств (А, В) подані на рис. 9.47. Таким чином, лінійні дискримінантні функції мають такий вигляд:

\[ y_1 = -192,407 + 10,612 \cdot x_1 + 296,274 \cdot x_2 + 39,474 \cdot x_3 + 26,162 \cdot x_4 + 3,73 \cdot x_5; \\ y_2 = -169,687 + 7,545 \cdot x_1 + 307,087 \cdot x_2 + 37,105 \cdot x_3 + 22,849 \cdot x_4 + 2,123 \cdot x_5. \]

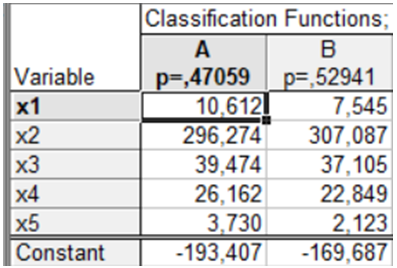
Рис. 9.47: Дискримінантні функції

Класифікаційна матриця (Classification matrix) містить інформацію про кількість і відсоток коректно класифікованих спостережень у кожній з груп. Рядки матриці — вихідні класи, стовпці — розпізнані класи за моделлю (рис. 9.48).

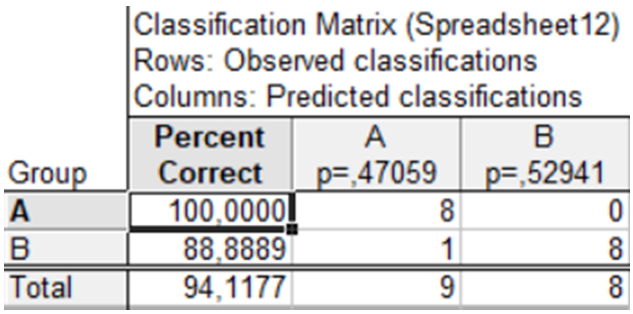
Рис. 9.48: Матриця класифікацій

Для визначення приналежності об’єкта до одного з виділених класів на основі побудованої дискримінантної моделі необхідно скористатися такими опціями:

1. Classification of cases (Класифікація спостережень) — таблиця класифікації для кожного спостереження.
2. Squared Mahalanobis distances (Квадрати відстаней Махаланобіса) — таблиця квадратів відстаней Махаланобіса для кожного спостереження до центру відповідної групи.
3. Posterior probabilities (Апостеріорні ймовірності) — таблиця апостеріорних ймовірностей приналежності кожного спостереження до відповідної групи.

Реалізація даного напряму аналізу подана на рис. 9.49. Об’єкти, які неправильно класифіковані, будуть відмічені (*).

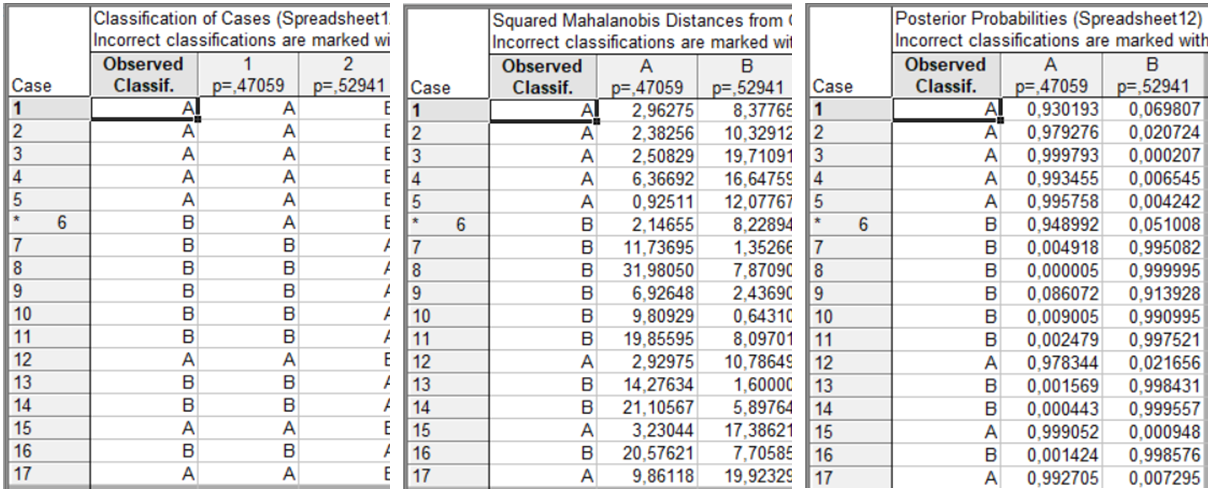
Рис. 9.49: Матриці розпізнавання стану підприємств

Більш детальний аналіз змінних передбачає побудову моделей за методами покрокового включення та виключення незалежних змінних.

У даному модулі реалізовано метод покрокового включення змінних (Forward stepwise) і метод покрокового виключення (Backward stepwise). Вибір методів здійснюється на стартовій панелі модуля ініціюванням опції Advanced options (stepwise analysis) (рис. 9.50).

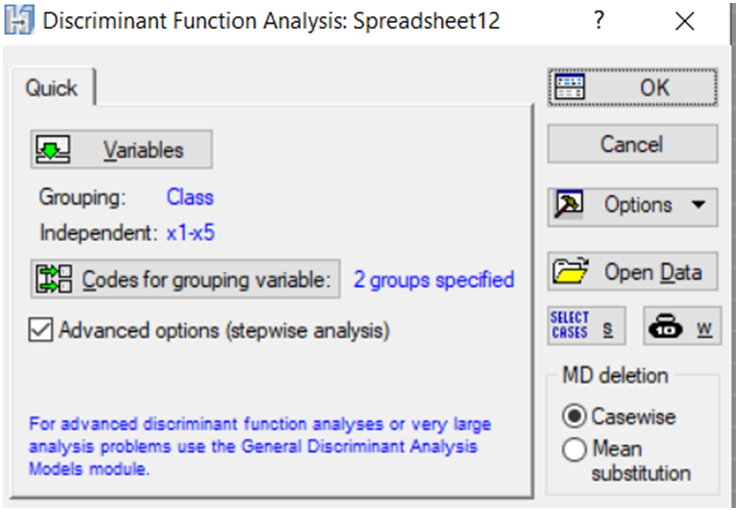
Рис. 9.50: Вибір опцій покрокового аналізу

Вибір методу оцінювання, порогові значення \(F\)-критерію включення або виключення, послідовність подання результатів вибирається у вкладці Advanced (рис. 9.51).

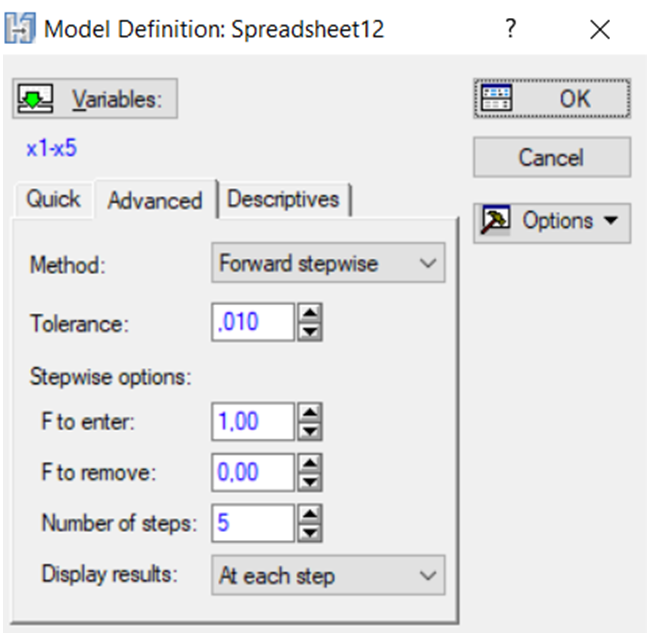
Рис. 9.51: Вибір методу покрокового дискримінантного аналізу

Послідовність етапів реалізації алгоритму покрокового включення (Forward stepwise) подано на рис. 9.52.

Рис. 9.52: Реалізація моделі покрокового включення змінних

Опції аналізу змінних, які ввійшли в модель (Variables in the model) і виключені з моделі (Variables not in the model), показані на рис. 9.53. Результати аналізу змінних за методом покрокового включення змінних подані на рис. 9.54,  9.55.

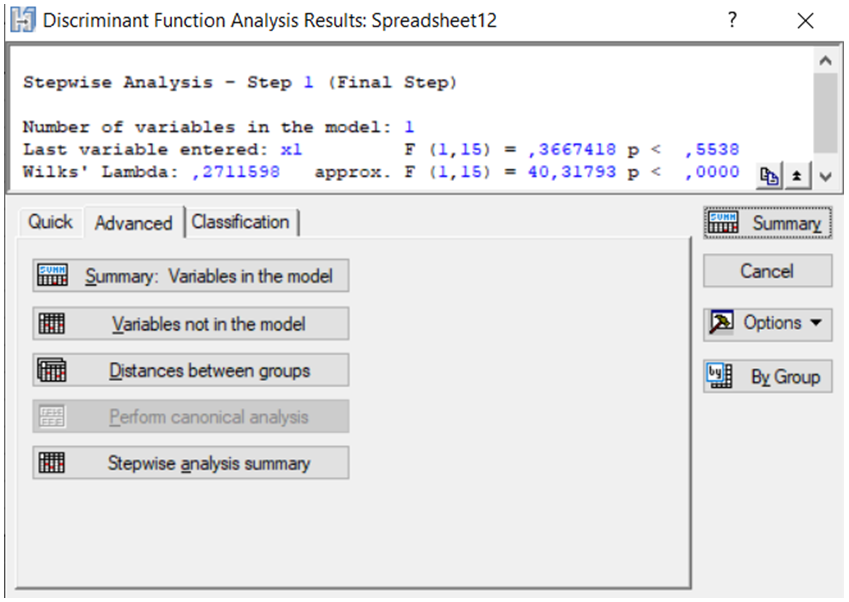
Рис. 9.53: Опції аналізу змінних

Рис. 9.54: Аналіз змінних у моделі

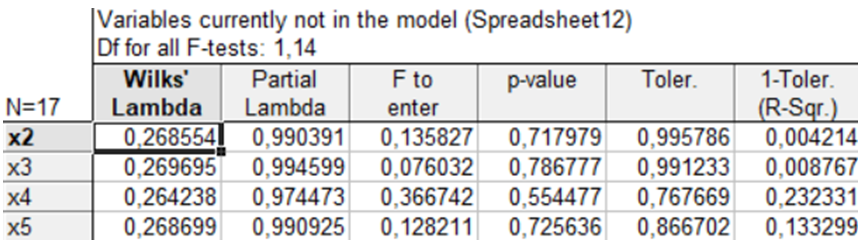
Рис. 9.55: Аналіз змінних, виключених з моделі

Аналіз змінних у моделі методом покрокового виключення подано на рис. 9.56.

Рис. 9.56: Аналіз змінних у моделі методом покрокового виключення

Для розпізнавання нових об’єктів (підприємств) на основі відомих значень коефіцієнтів необхідно в початкову таблицю вхідних даних додати нові спостереження (рис. 9.57).

Рис. 9.57: Вхідні дані для розпізнавання

Для визначення приналежності нових об’єктів до виділених класів необхідно скористатися такими опціями: Classification of cases (Класифікація спостережень); Squared Mahalanobis distances (Квадрати відстаней Махаланобіса); Posterior probabilities (Апостеріорні ймовірності). Результати розпізнавання наведено на рис. 9.58.

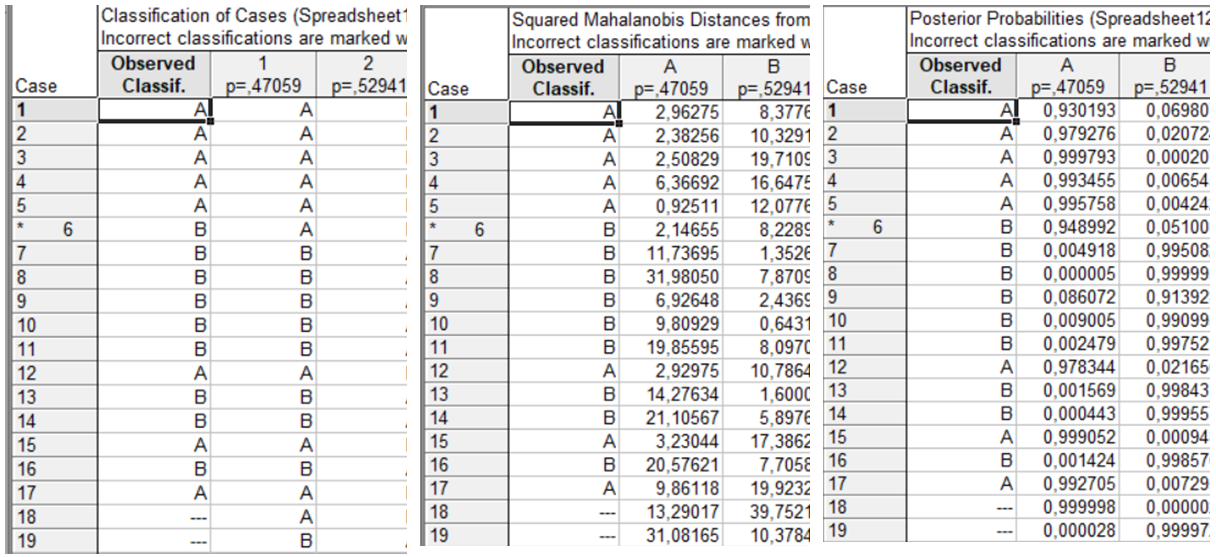
Рис. 9.58: Результати розпізнавання

Таким чином, можна зробити висновок, що підприємство №18 з зазначеними характеристиками належить до класу А (інвестиційно привабливі підприємства), а підприємство №19 — до класу В (підприємства-аутсайдери).

Діаграму розсіву об’єктів у просторі канонічних коренів можна побудувати натисканням кнопки Scatterplot of canonical scores в опції аналізу Perform canonical analysis (Канонічний аналіз) на вкладці Сanonical scores (рис. 9.59).

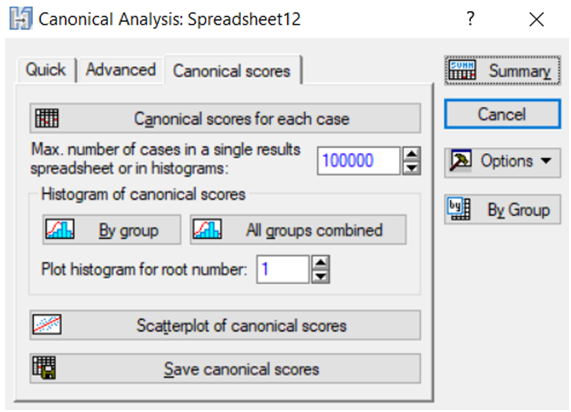
Рис. 9.59: Опції побудови діаграми

Таким чином, два нові підприємства за результатами аналізу відносяться відповідно до класу А та класу В.