9.1 Оцінка параметрів розподілу випадкових величин

Мета

Закріплення теоретичного та практичного матеріалу з оцінювання параметрів розподілу випадкових величин; набуття навичок роботи в модулі Basic Statistics / Tables.

Завдання

Необхідно провести аналіз варіаційного ряду для вибіркових даних у модулі Basic Statistics / Tables ППП Statistica:

1. Розрахувати статистичні характеристики ряду (середнє, дисперсію, середнє квадратичне відхилення, моду, медіану, розмах варіації, коефіцієнти асиметрії та ексцесу).
2. Побудувати гістограму та полігон розподілу випадкової величини, зробити висновки щодо характеру закону розподілу.
3. За допомогою критеріїв Пірсона та Колмогорова-Смірнова перевірити гіпотезу про нормальний закон розподілу.
4. Зробити висновки щодо групування об’єктів за величиною відповідного показника.

Література: [5–9; 14; 41–44; 48; 49; 76].

Методичні рекомендації

Для розв’язання та аналізу задач розглядуваного типу в ППП Statistica передбачений модуль Basic Statistics / Tables (Основні статистики й таблиці). Розглянемо порядок роботи в даному модулі.

У меню програм слід вибрати програму Statistica, після її запуску виберіть у меню пункт File / New для підготовки власних даних. Перед вами з’явиться діалогове вікно, у якому необхідно вказати кількість змінних (Number of variables) і кількість випадків (Number of Cases). Після введення натисніть кнопку вікна OK (рис. 9.1).

Рис. 9.1: Визначення кількості змінних і спостережень

Перед вами з’явиться порожнє поле, що містить таблицю розміром 25×2: 25 спостережень, 2 змінні (рис. 9.2). Кожен елемент даних, тобто значення показника, займає одну комірку поля даних.

Рис. 9.2: Поле даних

Після заповнення всіх комірок поля даних ви отримаєте таблицю, наведену на рис. 9.3.

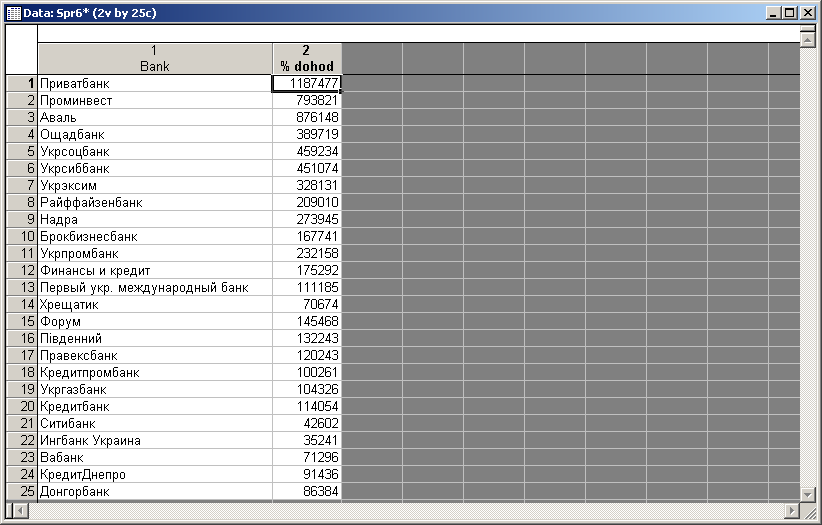
Рис. 9.3: Вихідні дані

Розрахуємо основні статистичні характеристики ряду (середнє, дисперсію, середнє квадратичне відхилення, моду, медіану, розмах, коефіцієнти асиметрії й ексцесу).

Щоб почати обчислювальні процедури, необхідно ввійти в позицію меню Statistics / Basic Statistics / Tables (рис. 9.4).

Рис. 9.4: Вибір модуля

Після підтвердження вибору модуля перед вами з’явиться діалогове вікно, що дозволяє задати напрям аналізу Descriptive statistics (Описові статистики), подане на рис. 9.5.

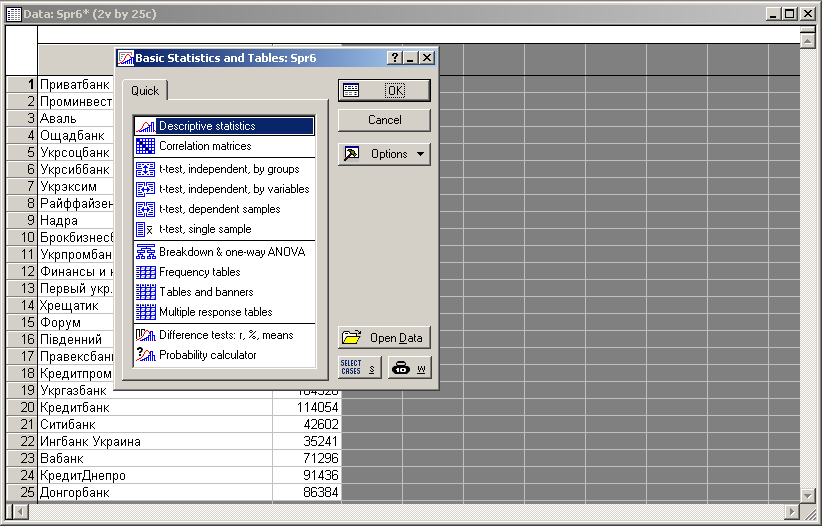
Рис. 9.5: Вибір напряму аналізу

Після вибору напряму аналізу з’явиться стартова панель модуля, де необхідно задати вихідні параметри: Variable (Змінні) та відповідний набір процедур для подальшого аналізу (рис. 9.6).

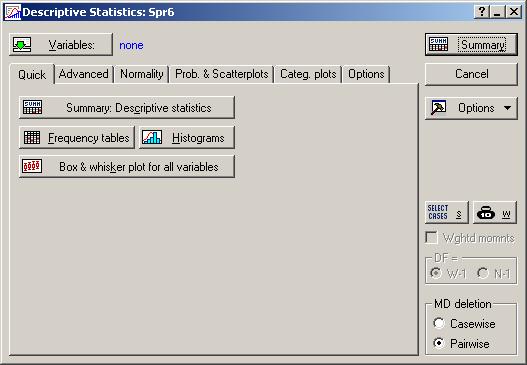
Рис. 9.6: Стартова панель модуля

Ініціюйте кнопку Variable (Змінні) й у вікні, що з’явилося, укажіть показники, за якими здійснюється аналіз. Після зазначення змінних підтвердіть свій вибір натисканням кнопки ОК. Далі, ініціювавши вкладиш Advanced, необхідно виділити основні статистики для розрахунку (рис. 9.7).

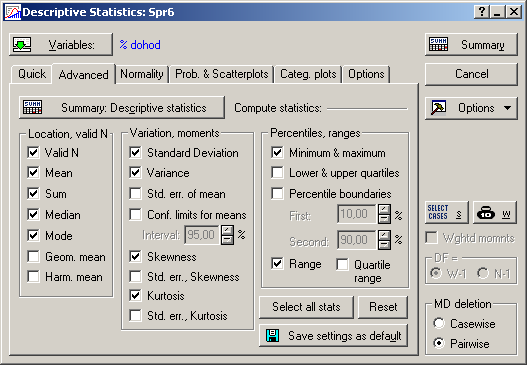
Рис. 9.7: Вибір описових статистик

Такими є: Valid N (кількість спостережень), Mean (середнє), Sum (сума значень), Median (медіана), Mode (мода), Standard Deviation (середнє квадратичне відхилення), Variance (дисперсія), Skewness (коефіцієнт асиметрії), Kurtosis (коефіцієнт ексцесу), Min & Max (мінімум і максимум), Range (розмах вибірки). Результати розрахунку описових статистик для даної вибірки отримуємо натисканням клавіші Summary (рис. 9.8).

Рис. 9.8: Описові статистики

Побудуємо гістограму та полігон розподілу випадкової величини; проведемо групування вибірки. Для наочності подання досліджуваної сукупності побудуємо полігон розподілу. Для цього необхідно зайти в меню Graphs / 2D Graphs / Scaterplots (рис. 9.9), вибрати змінні та задати параметри графіка (рис. 9.10) і побудувати полігон розподілу випадкової величини (рис. 9.11).

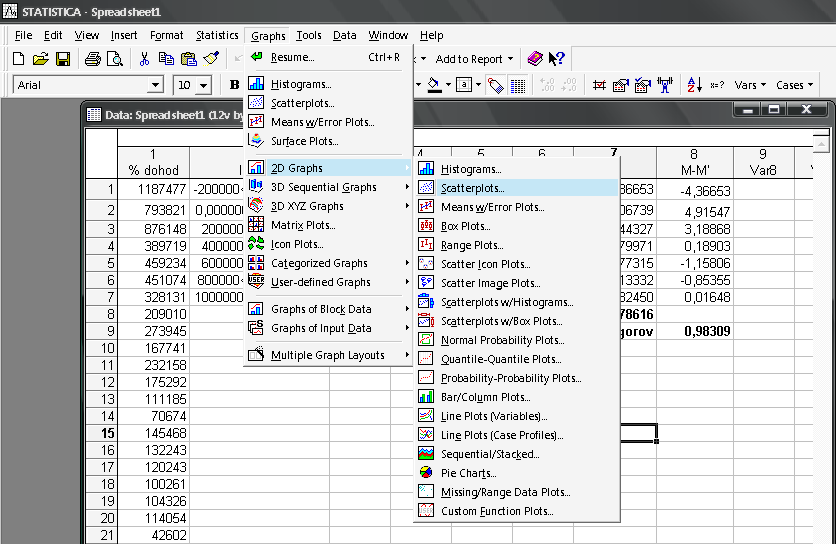
Рис. 9.9: Вибір типу графіка

Рис. 9.10: Вибір параметрів графіка

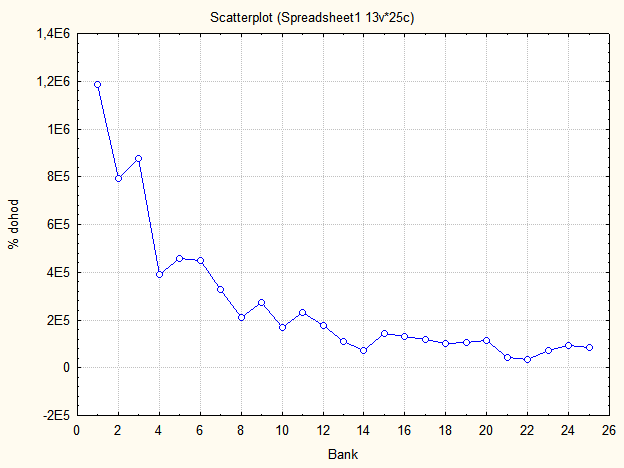
Рис. 9.11: Полігон розподілу випадкової величини

Подальший аналіз здійснюється в рамках перевірки вибірки на нормальний закон розподілу. Для проведення групування вибірки в стартовій панелі модуля вибираємо вкладиш Normality, де можна задавати бажану кількість інтервалів і критерій Колмогорова-Смірнова для тестування вибірки (рис. 9.12).

Рис. 9.12: Вибір параметрів групування випадкової величини

Натиснувши клавішу Frequency tables (Таблиці частот), отримуємо наступну таблицю (рис. 9.13).

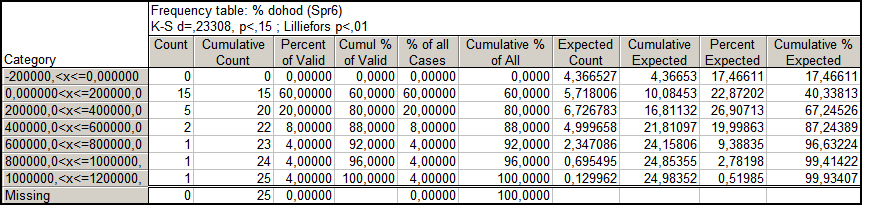
Рис. 9.13: Результат групування вибірки

Як видно, вихідна сукупність із двадцяти п’яти банків розбита на сім інтервалів. У кожному інтервалі розраховані такі характеристики: Count (частота), Cumulative Count (накопичена частота), Percent of Valid (% від загальної частоти), Cumul % of Valid (накопичений % від загальної частоти), % of all Cases (% від загального числа спостережень), Cumulative % of all Cases (накопичений % від загального числа спостережень), Expected Count (теоретична частота), Cumulative Expected (накопичена теоретична частота), % Expected (% від загальної теоретичної частоти), Cumulative % Expected (накопичений % від загальної теоретичної частоти).

Натиснувши клавішу Histograms (вкладиш Normality), створимо наступну гістограму розподілу з накладеною кривою нормального закону розподілу (рис. 9.14).

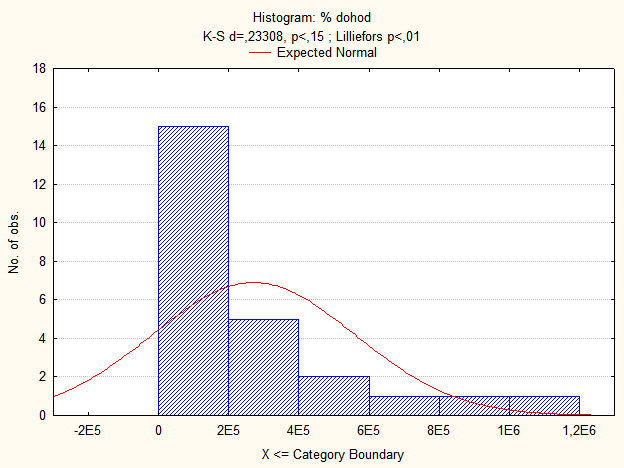
Рис. 9.14: Гістограма розподілу

Подальший аналіз вибірки передбачає розрахунок критерію Пірсона та Колмогорова-Смірнова для формування відповідних висновків про характер закону розподілу. Для визначення характеру закону розподілу та його відповідності нормальному закону дослідимо за допомогою графіків порівняння емпіричних і теоретичних частот і накопичених частот. Вихідні дані для побудови графіків та розраховані значення критерію Пірсона та Колмогорова-Смірнова наведені на рис. 9.15.

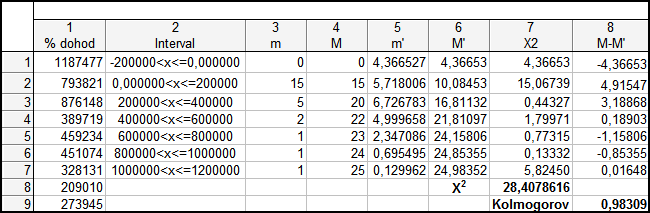
Рис. 9.15: Аналіз закону розподілу випадкової величини

Для побудови графіків інтервальних значень частоти розподілу досліджуваної сукупності необхідно зайти в меню Graphs / 2D Graphs / Scaterplots, вибрати змінні та задати параметри графіка (рис. 9.16).

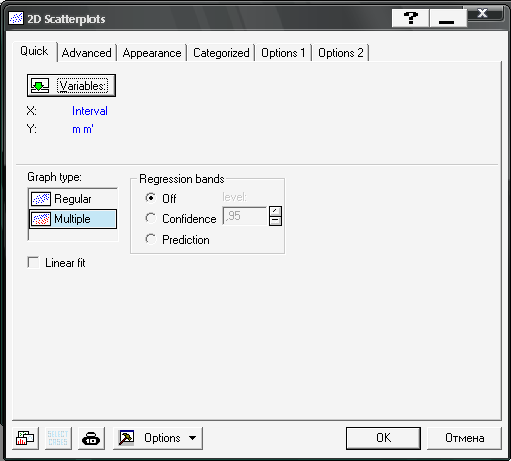
Рис. 9.16: Вибір змінних для побудови графіків

На рис. 9.17 і рис. 9.18 наведені графіки порівняння емпіричних і теоретичних частот і накопичених емпіричних і теоретичних частот, які дозволяють зробити висновки про відповідність нормальному закону розподілу та визначити розбіжність частот у кожному з досліджуваних інтервалів.

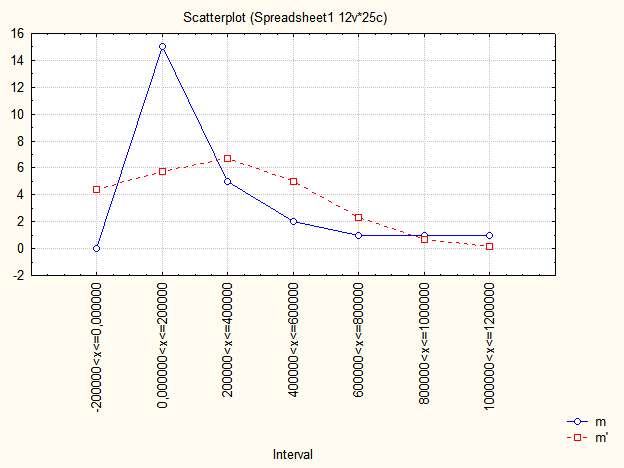
Рис. 9.17: Графік порівняння емпіричних і теоретичних частот

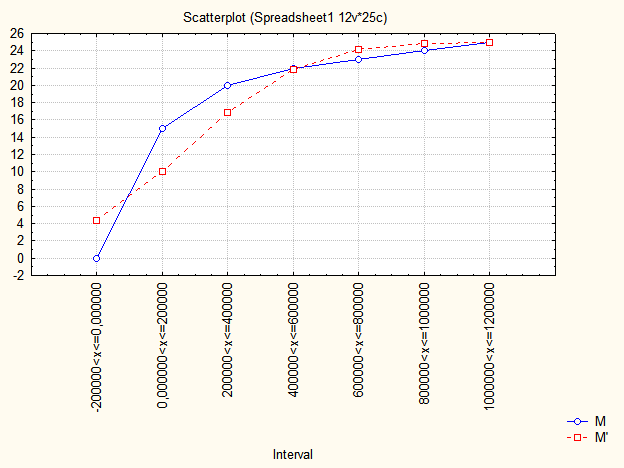
Рис. 9.18: Графік порівняння накопичених емпіричних і теоретичних частот

Далі робимо висновки про угрупування даних об’єктів за величиною показника % доходу. Порівнюємо отримані значення з табличними за відповідними критеріями та робимо висновки про характер закону розподілу.