9.2 Методи та моделі кластерного аналізу.
Класифікація без навчання

Мета

Закріплення теоретичного та практичного матеріалу за темою «Методи кластерного аналізу. Класифікація без навчання»; набуття навичок роботи в модулі Cluster Analysis.

Завдання

Необхідно побудувати моделі класифікації підприємств, використовуючи різні методи та стратегії класифікації для вибіркових даних в модулі Cluster Analysis ППП Statistica:

1. Побудувати моделі кластерного аналізу, використовуючи ієрархічні (деревоподібні) методи кластерного аналізу.
2. Порівняти результати дослідження за різними правилами об’єднання та використовуючи різні метрики. Побудувати різні типи дендрограм класифікації. Зробити висновки.
3. Провести класифікацію об’єктів за методом \(k\)-середніх, визначити характеристики моделі.
4. Проаналізувати результати класифікації з різним значенням виділених кластерів, побудувати графіки, привести основні статистики та оцінювання змінних за отриманими моделями.
5. Зробити висновки та подати економічну інтерпретацію отриманим результатам кластерних утворень.

Література: [5–9; 14; 41–44; 48; 49; 76].

Методичні рекомендації

Для розв’язання задач класифікації об’єктів у багатовимірному просторі та вивчення їх особливостей в ППП Statistica передбачений модуль Cluster Analysis (Кластерний аналіз). Розглянемо порядок роботи в даному модулі.

Таблиця вихідних даних для розв’язання задачі класифікації подана на рис. 9.19. Таким чином, задача дослідження полягає в отриманні класів однорідних об’єктів (підприємств) за такими показниками: \(x_1\) — продуктивність праці; \(x_2\) — коефіцієнт рентабельності капіталу; \(x_3\) — коефіцієнт фондовіддачі. Щоб приступити до обчислювальних процедур, необхідно ввійти в пункт меню Statistics / Multivariate Exploratory Techniques / Cluster Analysis (рис. 9.20).

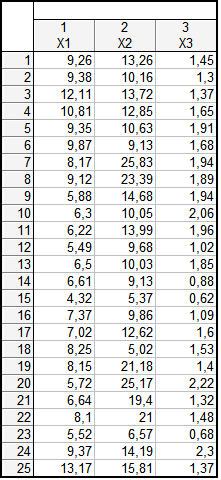
Рис. 9.19: Вихідні дані

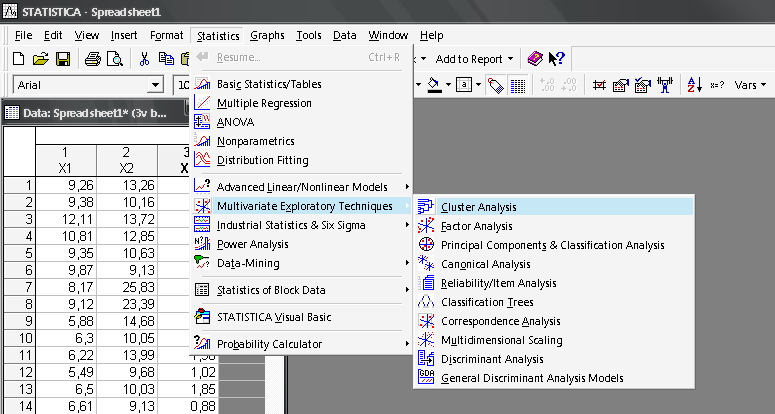
Рис. 9.20: Вибір модуля

Після підтвердження вибору модуля перед вами з’явиться стартова панель модуля (рис. 9.21), де необхідно вибрати напрям аналізу, тобто метод класифікації: Joining tree clustering — деревоподібна кластеризація; K-means clustering — метод \(k\)-середніх; Two-way joining — двовходова кластеризація.

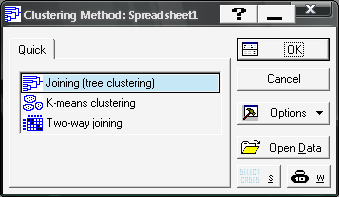
Рис. 9.21: Стартова панель модуля

Після підтвердження вибору методу (вибрано метод Joining tree clustering) необхідно задати вихідні параметри для проведення кластеризації (рис. 9.22): Variable (Змінні), Cluster (Об’єкти кластеризації), Amalgamation rule (Правила кластеризації), Distance measure (Міру подібності).

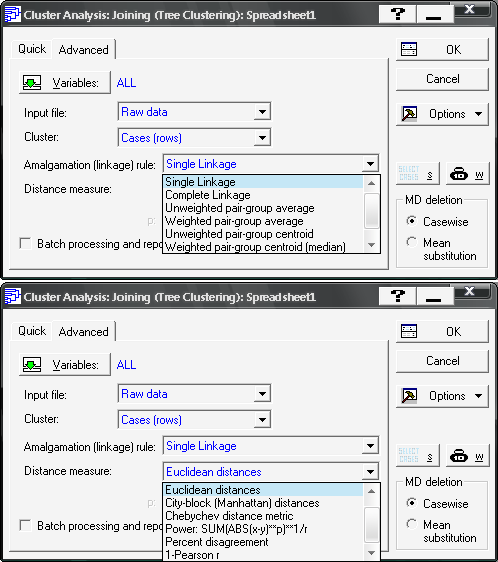
Рис. 9.22: Визначення вихідних параметрів

У розгядуваному модулі представлено такі правила ієрархічного об’єднання:

1. Single linkage — одиночного зв’язку;
2. Complete linkage — повних зв’язків;
3. Unweighted pair-group average — незваженого попарного середнього;
4. Weighted pair-group average — зваженого попарного середнього;
5. Unweighted pair-group centroid — незваженого центроїдного;
6. Weighted pair-group centroid — зваженого центроїдного;
7. Ward’s method — метод Уорда.

В якості міри подібності використовують метрики:

1. Euclidean distances — евклідова метрика;
2. Square Euclidean distances — квадрат евклідової метрики;
3. City-block (Manhattan) distances — Мангеттенська відстань;
4. Chebychev distances metric — відстань Чебишева;
5. Power metric — степенева відстань Мінковського;
6. Percent disagreement — відсоток незгоди (для категоріальних даних)
7. 1-Pearson r — 1-коефіцієнт кореляції Пірсона.

Для дослідження виберемо процедуру Single linkage (одиночного зв’язку) та звичайну евклідову метрику (Euclidean distances). Підтверджуючи вибір, натисніть клавішу (OK). З’явиться вікно результатів, де в верхній частині подана основна інформація та вибрані процедури дослідження. Опції в нижній частині вікна на вкладці Advanced призначені для аналізу результатів кластеризації (рис. 9.23): Horizontal hierarchical tree plot (горизонтальна деревоподібна діаграма); Vertical icicle plot (вертикальна деревоподібна діаграма — дендрограма); Amalgamation schedule (правило об’єднання в кластери); Graf of amalgamation schedule (графік порядку об’єднання); Distance matrix (матриця відстаней); Descriptive statistics (описові статистики).

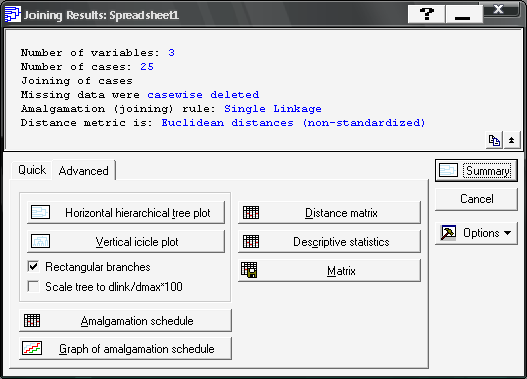
Рис. 9.23: Опції аналізу результатів

Натиснувши клавішу Vertical icicle plot, отримаємо дендрограму класифікації (рис. 9.24), де на осі абсцис подані об’єкти дослідження, а на осі ординат — відстані між ними.

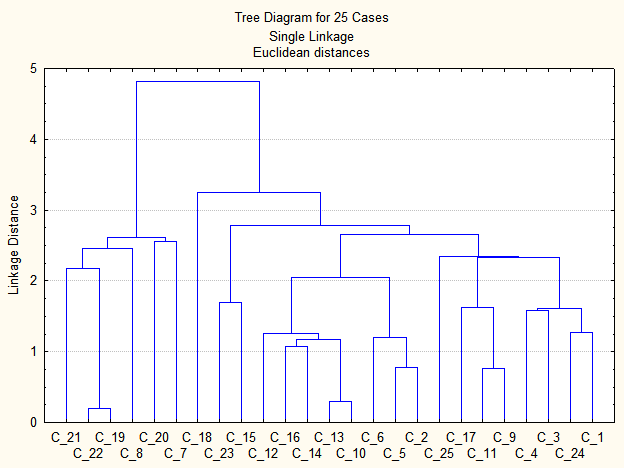
Рис. 9.24: Дендрограма класифікації

Натиснувши клавішу Distance matrix, отримаємо матрицю відстаней, фрагмент якої наведено на рис. 9.25. На рис. 9.26 наведено фрагмент матриці об’єднання (Amalgamation schedule).

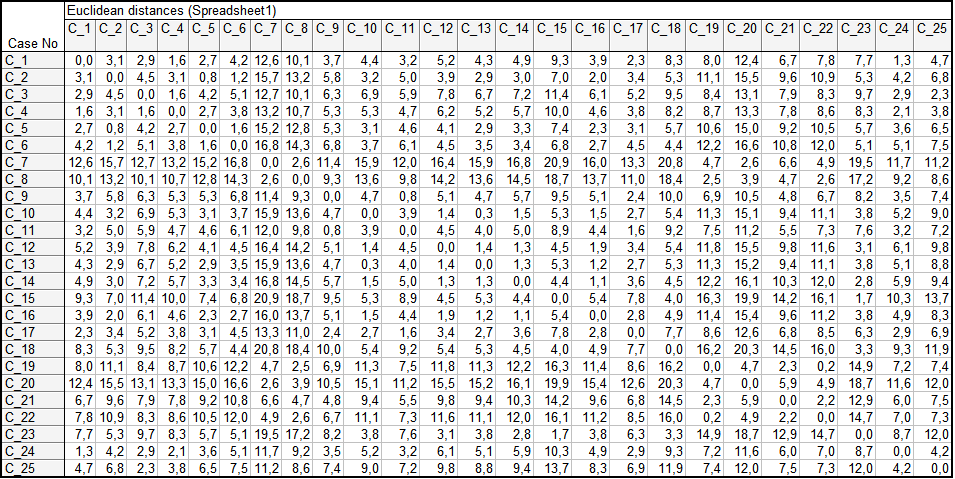
Рис. 9.25: Матриця відстаней

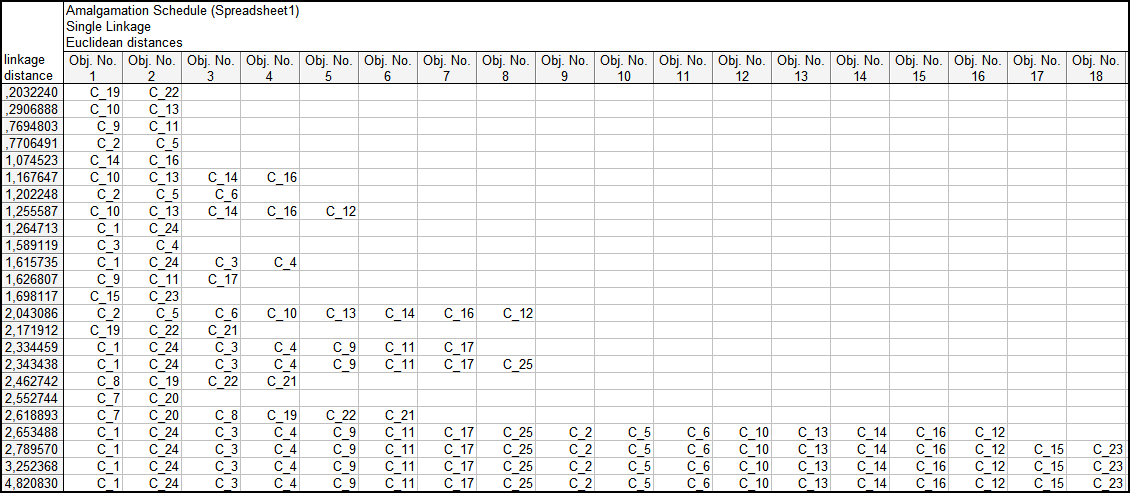
Рис. 9.26: Матриця об’єднання

Дендрограма класифікації за методом Уорда наведена на рис. 9.27. Аналіз дендрограми дозволяє розпізнати три групи (кластери) однорідних станів в спостережуваній сукупності даних.

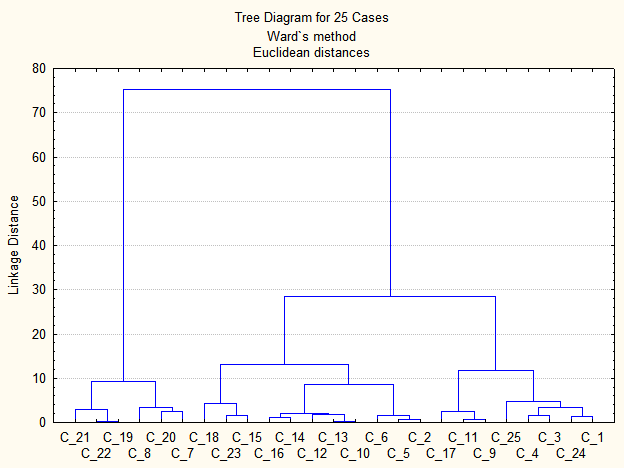
Рис. 9.27: Дендрограма класифікації за методом Уорда

Розглянемо реалізацію методу \(k\)-середніх (K-means clustering). Вибір методу на стартовій панелі модуля (рис. 9.28). Ініціювавши дану опцію, отримаємо діалогове вікно реалізації методу, де на вкладці Advanced необхідно задати змінні для аналізу (Variables), об’єкти кластеризації (Cluster), число кластерів (Number of clusters), число ітерацій (Number of iterations), та початкові центри кластерів — опції (Initial cluster centers) (див. рис. 9.28).

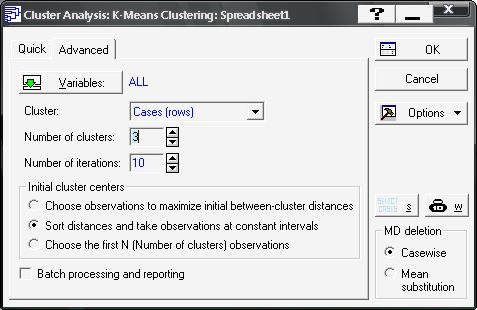
Рис. 9.28: Діалогове вікно методу \(k\)-середніх

Вікно аналізу результатів методу \(k\)-середніх наведено на рис. 9.29. Верхня частина є інформаційною, а нижня (вкладка Advanced) дозволяє отримати повну інформацію результатів аналізу. Розглянемо функціональне значення опцій даного вікна:

• Summary: Cluster means & Euclidean distances — евклідові відстані та середні значення станів кластерів;
• Analysis of variance — дисперсійний аналіз;
• Graf of means — графік середніх значень;
• Descriptive statistics for each cluster — описові статистики для кластерів;
• Members of each cluster & distances — члени кластерів та їх відстані до центру кластера;
• Save classifications and distances — збереження результатів кластеризації.

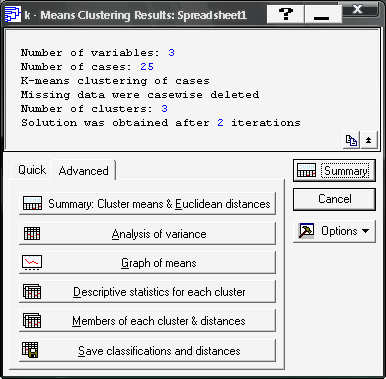
Рис. 9.29: Опції аналізу результатів методу \(k\)-середніх

Евклідові відстані між отриманими кластерами та середні значення для кожного досліджуваного показника подані на рис. 9.30, причому значення евклідових відстаней знаходяться під головною діагоналлю, а над нею — квадрат евклідових відстаней.

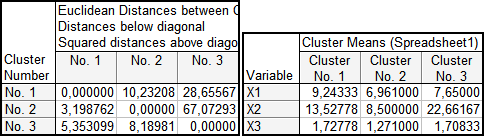
Рис. 9.30: Евклідові відстані та середні значення станів кластерів

Графік середніх значень для кластерів станів приведено на рис. 9.31. Як видно, найбільше кластери відрізняються за показником \(x_2\), потім \(x_1\) і дуже малі відмінності в середніх для показника \(x_3\).

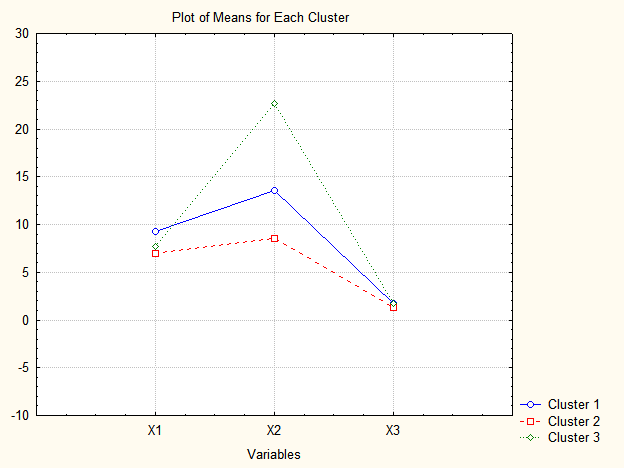
Рис. 9.31: Графік середніх значень для кластерів станів

Результати дисперсійного аналізу оцінки якості показників наведено на рис. 9.32. У таблиці наведені значення міжгрупових і внутрішньогрупових дисперсій ознак. Чим менше значення внутрішньогрупової дисперсії і більше значення міжгрупової, тим краще ознака характеризує приналежність об’єктів до кластера. Параметри \(F\) і \(p\) визначають внесок ознаки в класифікацію.

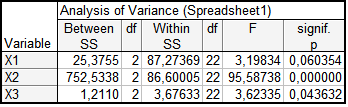
Рис. 9.32: Таблиця дисперсійного аналізу

На рис. 9.33. показані описові статистики для виділених кластерів, а саме: середнє, середньоквадратичне відхилення та дисперсія.

Рис. 9.33: Описові статистики для кластерів

Члени кластерів та їх відстані до центру відповідного кластеру наведено на рис. 9.34. Таким чином, дані таблиці дозволяють визначити склад кожного кластера.

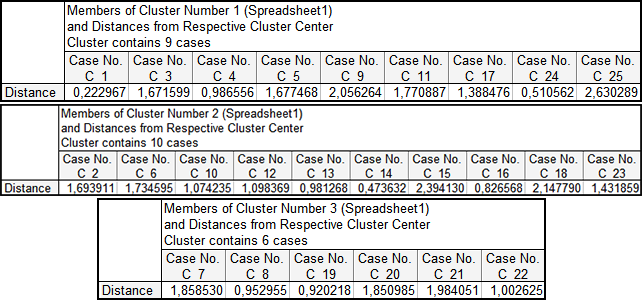
Рис. 9.34: Члени кластерів та їх відстані до центру кластера

Так, кластер №3 (шість підприємств) має найвищій рівень рентабельності, а показники продуктивності праці та фондовіддача знаходяться на середньому рівні. Кластеру №1 (дев’ять підприємств) властиві найвищі показники продуктивності праці та фондовіддачі з середнім значенням рентабельності капіталу. Кластеру №2 (десять підприємств) притаманні найнижчі значення за всіма досліджуваними показниками.