2.3. Теорема додавання ймовірностей

Під теоремою додавання ймовірностей мають на увазі ймовірність суми сумісних подій. Згадаємо, що ймовірність суми несумісних подій визначається аксіомою IV, за якою ймовірність суми несумісних випадкових подій \(A\) та \(B\) дорівнює сумі їх безумовних ймовірностей.

Згадаємо, що ймовірність суми несумісних подій визначається аксіомою IV, за якою ймовірність суми несумісних випадкових подій \(A\) та \(B\) дорівнює сумі їх безумовних ймовірностей.

Теорема

Ймовірність появи хоча б однієї з двох сумісних подій дорівнює сумі їх ймовірностей за виключенням ймовірності їх добутку (2.9).

\[\begin{equation} P(A+B)=P(A)+P(B)-P(AB) \tag{2.9} \end{equation}\]

Доведення

Для доведення цієї теореми скористуємося діаграмою Венна – Ейлера (рис. 2.1), на якій сумі сумісних подій \(A\) і \(B\) відповідає площа заштрихованої фігури – кругів, що перетинаються. Ця фігура складається з трьох частин, які можна розглядати як несумісні події. Одна з цих частин (зліва направо) є частиною круга, що відповідає події \(A\) за умови, що подія \(B\) не відбулась, тобто за виключенням події \(B\). Це подія \(A\backslash B\). Друга – це перетин кругів \(A\) і \(B\), тобто подія \(AB\), яка полягає в одночасній появі подій \(A\) і \(B.\) Нарешті третя складова – це частина круга, що відповідає події \(B\) за виключенням події \(A\), тобто \(B\backslash A.\)

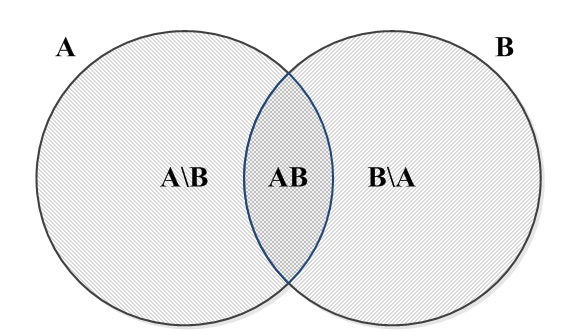
Рис. 2.1. Сума сумісних подій A i B як сукупність несумісних подій A\B, B\A та AB

Випадкову подію \(A\backslash B\) можна надати як добуток подій \(A\) та \(\overline{{B}}\), тобто \(A\backslash B = A \cap \overline{B{}}\). Аналогічно \(B\backslash A = B \cap \overline{{A}}\). Отже, ймовірність суми двох сумісних подій можна розглядати як ймовірність суми трьох несумісних випадкових подій: \(P\left( A + B \right) =P(A\overline{{B}} + B\overline{{A}} + AB)\). Дійсно, усі ці три події є попарно несумісними. Так, у складі події \(AB\) міститься подія \(B,\) а у складі події \(A\overline{{B}}\) – подія \(\overline{{B}}\). Оскільки події \(B\) і \(\overline{{B}}\) є несумісними, то також несумісними є події \(AB\) і \(\overline{A{B}}.\) Застосувавши для суми несумісних подій аксіому IV, маємо:\[P\left( A + B \right) = P\left( A\overline{{B}} \right) + P\left( B\overline{{A}} \right) + P(AB).\]

Зазначимо, що \(P\left( A\overline{B} \right) + P\left( \text{AB} \right) = P(A)\) та \(P\left( B\overline{A} \right) + P\left( \text{AB} \right)=P(B).\) Підставивши обидва ці вирази у попередню формулу, отримаємо, що \[P\Big(A+B\Big)=\left(P\Big(A\overline{B} \Big)+P\Big( \text{AB} \Big) \right)+\left(P\Big( B\overline{A} \Big) + P\Big( \text{AB} \Big) \right)-P\Big( \text{AB} \Big) = P\Big(A \Big)+P\Big(B \Big)-P\Big(AB\Big).\] Це і треба було довести.

Зауваження

У деяких підручниках формула для визначення добутку несумісних подій розглядається як наслідок формули (2.1) у випадку, коли \(P(AB)=0.\) Однак при аксіоматичній побудові теорії ймовірностей при доведенні формули (2.1) користуються положенням аксіоми IV.

Для довільної кількості подій теорема додавання ймовірностей набуває вигляду (2.10):

\[\begin{equation} P(\sum_{i = 1}^{n}{S_{i}) = \sum_{i}^{}{P(S_{i}) - \sum_{i,j}^{}{P\left( S_{i}S_{j} \right) + \cdots + \left( - 1 \right)^{n - 1}P(S_{1}S_{2}\cdots S_{n})}}}. \tag{2.10} \end{equation}\]

Розглянемо застосування наведених вище теорем.

Приклад 2.5

Деякий виріб складається з трьох компонентів, які виготовляють різні цехи підприємства. Ймовірність того, що продукція не відповідає стандарту, становить 0,2 для першого цеху, для другого цеху – 0,1, для третього – 0,3. Визначити ймовірність того, що готовий виріб буде мати лише один дефектний компонент.

Розв’язання

Для наочності проілюструємо умову прикладу за допомогою діаграми Венна – Ейлера (рис.2.2), де площа круга \(A_{i}\ (i={1,2,3})\) відповідає ймовірності \(P(A_{i})\) того, що нестандартна продукція виготовлена саме \(i\)-им цехом, а площа прямокутника, який описує простір елементарних подій, дорівнює одиниці.

Ймовірність події, яка полягає в тому, що неякісною є продукція тільки будь-якого одного цеху, вимірюється як площа фігури, яка складається з частин кожного з трьох кругів, що заштриховані лише в одному напрямку. Отже, ймовірність події \(A\), яка полягає в тому, що продукція тільки одного цеха буде неякісною, визначається співвідношенням:

\[P\left( A \right) = P(A_{1}\overline{A_{2}}\ \overline{A_{3}} + \overline{A_{1}}A_{2}\ \overline{A_{3}} + \ \overline{A_{1}} \ \overline{A_{2}}\ A_{3}).\]

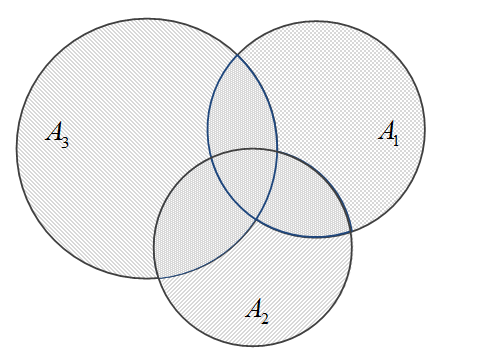
Рис. 2.2. Діаграма Венна-Ейлера для трьох сумісних подій

Оскільки всі події є незалежними і попарно несумісними, то ймовірність їх суми за аксіомою IV дорівнює сумі їх ймовірностей, тобто:

\[P\left( A \right) = P\left( A_{1} \right)P\left( \overline{A_{2}}\right)P\left( \overline{A_{3}} \right)+P\left(\overline{A_{1}} \right)P\left( A_{2}\right)P\left(\overline{A_{3}}\right)+P(\overline{A_{1}})P(\overline{A_{2}})P(A_{3}).\]

Ймовірність того, що продукція \(i\)-го цеха буде якісною, тобто випадкової події, яка є протилежною події \(A_{i}\) (продукція \(i\)-гo цеха не відповідає стандарту), становить: \[P\left( \overline{A_{i}} \right)= 1 - P(A_{i}).\]

Тоді ймовірність того, що готовий виріб буде мати лише один дефектний компонент, дорівнює:

\[P\left( A \right) = 0,2\cdot\left( 1 - 0,1 \right)\cdot\left( 1 - 0,3 \right) + \left( 1 - 0,2 \right)\cdot0,1\cdot\left( 1 - 0,3 \right)\ + \left( 1 - 0,2 \right)\cdot(1 - 0,1)\cdot 0,3 = 0,398.\]

Відповідь: ймовірність того, що готовий виріб буде мати лише один дефектний компонент, дорівнює 0,398.