1.4. Операції над подіями

Припустимо, що є простір елементарних подій \(\Omega\) довільної природи. Тобто він може бути скінченною або нескінченною, дискретною або неперервною множиною елементарних подій. На цьому просторі розглядатимемо випадкові події \(A,\ \ B,\ \ C,\ \ \ldots\), кожна з яких є підмножиною множини \(\Omega\). Отже, дії з подіями можна розглядати як дії з підмножинами.

Сума подій

Сумою подій \(A,\ \ B,\ \ C,\ \ \ldots\) є подія, яка полягає в тому, що матиме місце хоча б одна з випадкових подій, сума яких розглядається. Оскільки кожна з випадкових подій \(A,\ \ B,\ \ C,\ \ \ldots\) є підмножиною простору елементарних подій \(\Omega\), то сумою випадкових подій є подія, яка матиме місце, якщо відбуватиметься одна з елементарних подій, що входять до складу подій \(A,\ \ B,\ \ C,\ \ \ldots\). Зрозуміло, що в цьому сенсі сума подій є об’єднанням підмножин, які відповідають цим подіям.

На прикладі двох випадкових подій маємо:

\[\begin{equation} A + B = A \cup B. \tag{1.9} \end{equation}\]

Додавання подій передбачає, що результатом (їх сумою) може бути або подія \(A\), або подія \(B\), або обидві події одночасно, якщо вони сумісні. Відповідно, сумою випадкових подій є сукупність усіх елементарних подій, які є сприятливими для кожної окремої випадкової події цієї суми. На рис. 1.3 та рис. 1.4 наведені діаграми Венна–Ейлера, що відповідають додаванню множин.

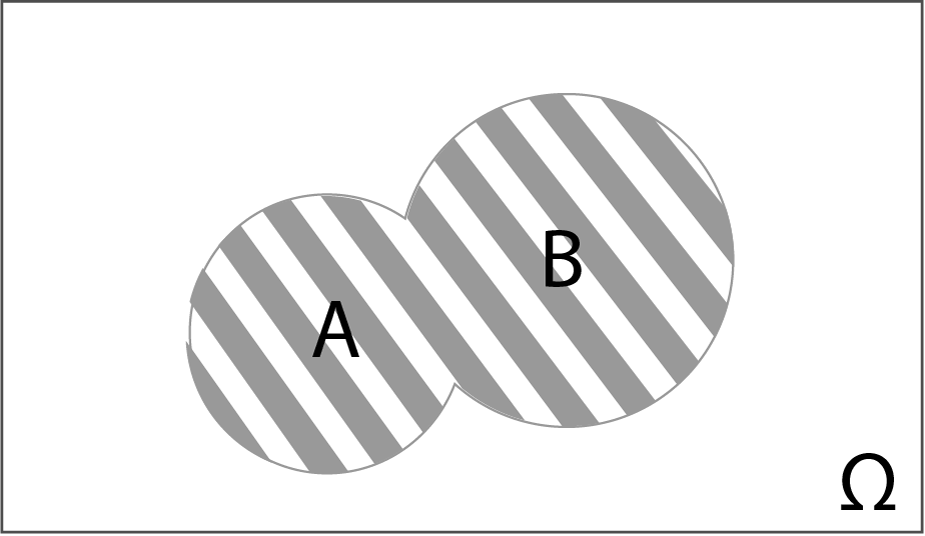
Рис. 1.3. Діаграма Венна – Ейлера, на якій надана сума сумісних випадкових подій

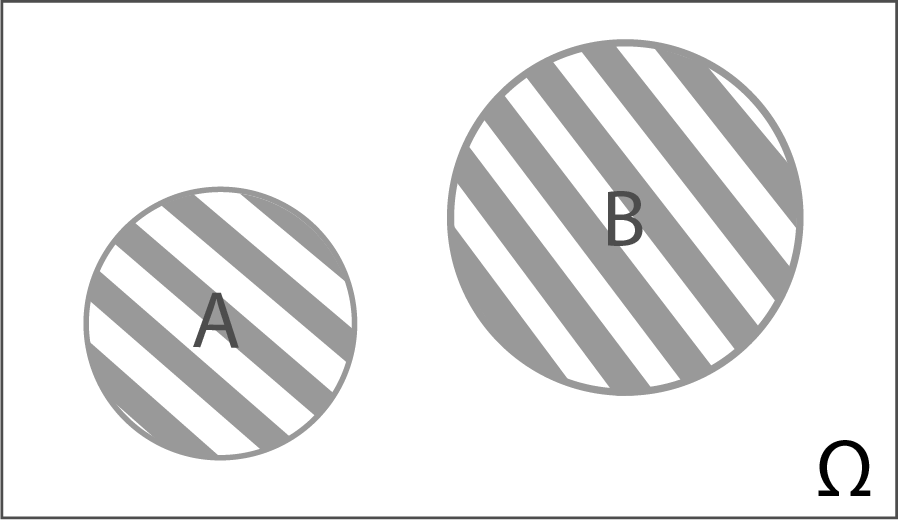
Рис. 1.4. Діаграма Венна – Ейлера, на якій надана сума несумісних випадкових подій

Якщо випадкові події є сумісними, то відповідні їм кола перетинаються, і їх перетин відображає ті з елементарних подій, які одночасно є сприятливими і для однієї, і для іншої з випадкових подій (рис. 1.3). Якщо ж випадкові події є несумісними, то відповідні їм кола не повинні перетинатися, оскільки на просторі елементарних подій \(\Omega\) не існують такі елементарні події, які б одночасно були сприятливими для обох випадкових подій (рис. 1.4).

Слід зазначити, що сумою протилежних подій є вірогідна подія, оскільки до складу протилежної події входять усі ті елементарні події, які не увійшли у вихідну, тобто протилежна подія доповнює вихідну до повної групи несумісних подій:

\[A + \overline{A} = \Omega.\]

Приклад 1.4

У шухляді містяться чорні й білі кульки. З цієї шухляди навмання витягають дві кульки. Побудувати простір елементарних подій і навести приклад cуми випадкових подій на цьому просторі.

Розв’язання

Простір елементарних подій визначається чотирма елементарними подіями: \(\omega_{1} = \left\{ б;\ \ б \right\}\), коли обидні кульки є білими; \(\omega_{2} = \left\{ ч;\ \ б \right\}\), коли перша кулька є чорною, а друга – білою; \(\omega_{3} = \left\{ б;\ \ ч \right\}\), коли перша кулька є білою, а друга – чорною; \(\omega_{4} = \left\{ ч;\ \ ч \right\}\), коли обидні кульки є чорними. Нехай випадкова подія \(A\) полягає в тому, що перша кулька є білою, тобто \(A = \left\{ \omega_{1};\ \ \omega_{3} \right\}\), а випадкова подія \(B\) – у тому, що кульки матимуть різний колір, тобто \(B = \left\{ \omega_{2};\ \ \omega_{3} \right\}\). Тоді випадкову подію \(C = \{\omega_{1},\ \ \omega_{2},\ \ \omega_{3}\}\), яка полягає у тому, що хоча б одна кулька буде білою, можна представити як суму випадкових подій \(A\) та \(B\):

\[C = A + B = \{\omega_{1},\ \ \omega_{3}\} \cup \{\omega_{2},\ \ \omega_{3}\} =\{\omega_{1},\ \ \omega_{2},\ \ \omega_{3}\}.\]

Зверніть увагу, що випадкові події \(A\) та \(B\) є сумісними, оскільки елементарна подія \(\omega_{3}\) є сприятливою для появи як події \(A\), так і події \(B\), отже, сума множин складається з трьох елементарних подій.

Протилежною до випадкової події \(С = \{\omega_{1},\ \ \omega_{2},\ \ \omega_{3}\}\) є випадкова подія \(\overline{С} = \{\omega_{4}\}\), яка полягає у тому, що обидві кульки будуть чорними.

Знайдемо їх суму:

\[С + \overline{С} = \{\omega_{1},\ \ \omega_{2},\ \ \omega_{3}\} \cup \{\omega_{4}\} = \{\omega_{1},\ \ \omega_{2},\ \ \omega_{3},\ \ \omega_{4}\} = \Omega.\]

Отже, сума події \(C\) і протилежної до неї події \(\overline{C}\) є вірогідною подією. Оскільки події \(C\) і \(\overline{C}\) є несумісними, то вони утворюють повну групу несумісних подій.

Добуток подій

Добутком подій \(A,\ \ B,\ \ C,\ldots\) є подія, яка полягає в тому, що матимуть місце одночасно всі випадкові події, добуток яких розглядається. Тобто добуток випадкових подій є перетином підмножин, що їм відповідають: \[\begin{equation} A B = A \cap B. \tag{1.10} \end{equation}\]

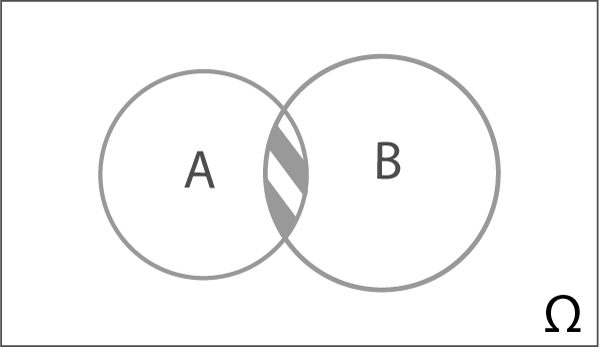
Рис. 1.5. Діаграма Венна – Ейлера, на якій надано добуток сумісних випадкових подій A та B

Добутком випадкових подій є така випадкова подія, коли одночасно мають місце випадкові події \(A\) і \(B\). Отже, для того, щоб ця множина не була порожньою, на множині елементарних подій \(\Omega\) повинна існувати хоча б одна елементарна подія, яка була б сприятливою для обох випадкових подій, добуток яких розглядається.

Оскільки випадкова подія \(S\) і протилежна їй випадкова подія \(\overline{S}\) за означенням не мають елементарних подій, які б були сприятливими для них обох (\(S\ \cap \overline{S} = \ Ø\)), то їх добуток є пустою множиною:

\[S\ \overline{S} = \ Ø.\]

Діаграма Венна–Ейлера

Приклад 1.5

У шухляді містяться чорні й білі кульки. З цієї шухляди навмання витягають дві кульки. Навести приклад добутку випадкових подій.

Розв’язання

Нехай випадкова подія \(A\) полягає в тому, що обидві кульки мають однаковий колір: \(A = \left\{ \omega_{1};\ \ \omega_{2} \right\}\), де \(\omega_{1} = \left\{ б;\ \ б \right\}\) та \(\omega_{2} = \left\{ ч;\ \ ч \right\}\). Подія \(B = \left\{ \omega_{1};\ \ \omega_{3};\ \ \omega_{4} \right\}\) полягає в тому, що хоча б одна кулька виявиться білою, отже, додаються події \(\omega_{3} = \left\{ б;\ \ ч \right\}\) та \(\omega_{4} = \left\{ ч;\ \ б \right\}\). Тоді перетином випадкових подій \(A = \left\{ \omega_{1};\ \ \omega_{2} \right\}\) і \(B = \left\{ \omega_{1};\ \ \omega_{3};\ \ \omega_{4} \right\}\) є елементарна подія \(\omega_{1}\):

\[A \cap B = \{\omega_{1};\ \ \omega_{2}\} \cap \{\omega_{1};\ \ \omega_{3};\ \ \omega_{4}\} = \omega_{1}.\]

Відповідь: добутком випадкових події \(A\) і \(B\) є елементарна подія \(\omega_{1}\), тобто обидві кульки є білими.

Різниця подій

Різницею подій \(B\) та \(А\) є така випадкова подія, для якої сприятливими є всі елементарні події, що є сприятливими для випадкової події \(B\), за винятком тих, які є сприятливими для випадкової події \(A\). Отже, маємо подію \(B\) за винятком подіїї \(A\): \[\begin{equation} B - A = B\backslash A \tag{1.11} \end{equation}\]

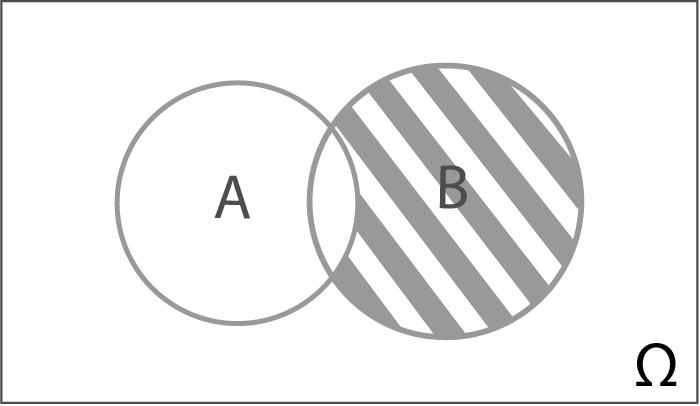
Рис. 1.6. Діаграма Венна – Ейлера, на якій надана різниця B \  A сумісних випадкових подій

За принципом різниці множин визначаються протилежні події. Так, \(\overline{A} = \Omega\backslash A\), тобто сприятливими для події \(\overline{A}\) є всі елементарні події простору \(\Omega\) за винятком тих, що входять до складу події \(A\).

Приклад 1.6

У шухляді містяться чорні й білі кульки. З цієї шухляди навмання витягають дві кульки. Навести приклад різниці двох випадкових подій.

Розв’язання

Якщо випадкова подія \(A = \left\{ \omega_{1};\ \ \omega_{2} \right\}\), де \(\omega_{1} = \left\{ б;\ \ б \right\}\) \(\omega_{2} = \left\{ ч;\ \ ч \right\}\), тобто полягає в тому, що обидві кульки мають однаковий колір, то на просторі елементарних подій \(\Omega = \left\{ \omega_{1};\ \ \omega_{2};\ \ \omega_{3};\ \ \omega_{4} \right\}\) протилежною є подія \(\overline{A} = \left\{ \omega_{3};\ \ \omega_{4} \right\}\), яка полягає в тому, що кольори кульок будуть різними. Подію \(\overline{A}\) можна розглядати як різницю між простором елементарних подій \(\Omega\) і випадковою подією \(A\) (до речі, це співпадає з означенням протилежної події).

Діаграма Венна–Ейлера

Варто зазначити, що це означення є справедливим і в граничних випадках. Наприклад, \(\overline{\Omega} = \Omega - \Omega = \ Ø\) або \(\Omega - \ Ø = \Omega.\)

Ми розглядали приклади, що стосуються дій з двома подіями. Такі ж принципи застосовуються і в тому випадку, коли розглядається більше подій. У цьому випадку для кращого розуміння дій над подіями їх доцільно подавати за допомогою діаграм Венна–Ейлера.

Приклад 1.7

На діаграмі Венна–Ейлера зображені випадкові події \(A\), \(B\) і \(C\). Визначити, чи правильно вказані дії над подіями, результат яких відповідає заштрихованим областям.

Приклад 1.8

Наведені дії над подіями, результат яких відповідає заштрихованим областям.